Ganar en el casino es un sueño compartido por muchos. Pero a menos que sean Gladstone, o que sepan que la ruleta está amañada (y cómo está amañada), no hay manera fácil de ganar. Sin embargo, si quieren aumentar sus posibilidades de hacerlo, puedo enseñarles cómo, pero pagando: pongan 50 € en un sobre y envíenmelo por correo. Al recibirlo, les revelaré el método… (es broma).
El hecho es que la extracción de diferentes números es independiente, lo que significa que cualquier secuencia tiene la misma probabilidad de salir, en cualquier momento. Obviamente esto no está de acuerdo con nuestra experiencia. Para simplificar, juguemos por ahora sólo en rojo o negro, o “manque” y “passe”, o pares e impares, o, lo que es lo mismo, cara y cruz con una moneda. Vamos a representar las dos opciones con los símbolos 0 y 1.
La primera pregunta que quizá nos podamos hacer es: ¿la secuencia “11111111” es más o menos probable que la secuencia “00101101”?
Si bien puede parecer imposible, ambas son igualmente probables, y la probabilidad es (1/2)8 = 1/256. La segunda parece más probable por dos razones: en primer lugar, es menos reconocible que la primera, por lo que tendemos a clasificarla en la clase de las secuencias “con más o menos el mismo número de unos y ceros”, y por supuesto, la probabilidad de sacar un secuencia así es mucho mayor que la extracción de la clase con el 100% de unos: en la primera clase (para 8 símbolos) hay 70 diferentes secuencias posibles, en la segunda sólo una. La segunda razón es que tenemos una idea equivocada de lo que “debería” ser al azar, que, por ejemplo, nos hace decir que las secuencias “01010101” o “00001111” son menos probables que “00101101”. [Falk, Ruma & Konold, Clifford E. (1997), “Making sense of randomness: Implicit encoding as a basis for judgment”, Psychological Review 104, 301-318. http://homepage.psy.utexas.edu/homepage/class/Psy355/Gilden/falk.pdf]
Sin embargo, estas consideraciones eliminan el método “esperar una larga secuencia de unos y luego apostar en 0”, y similares.
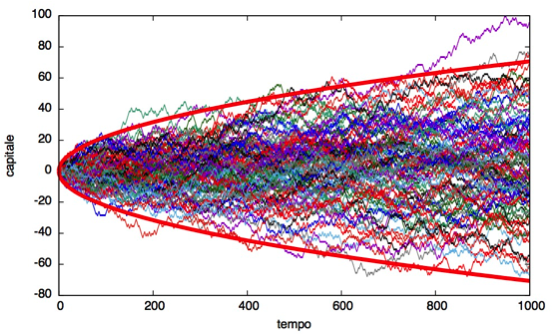
Apostando al azar (o incluso siempre al mismo número) no se deberían dar en promedio pérdidas o ganancias. En primer lugar en la ruleta hay un cero (y en la americanas doble cero), y entonces la suma de las probabilidades de pares e impares, por ejemplo, no es uno: en promedio siempre se pierde. Pero vamos a suponer que usted está jugando con cara y cruz y que siempre apuesta una unidad. Nuestro capital sigue lo que en términos técnicos se llama un paseo aleatorio, algo como en la figura 1 (sólo que en realidad se empieza con un cierto capital en lugar de cero).
El problema es que el paseo aleatorio no está limitado: es cierto que la media en tiempos largos, o después de muchas realizaciones, es cero, pero sus “fluctuaciones” crecen con el número de pasos. Esto significa que tarde o temprano nuestro capital será cero, momento en el que vamos a tener que tomar un préstamo. Y nuevamente, tarde o temprano nuestro capital se reducirá otra vez a cero, etc.
Dicho esto, la regla de “redoblar” (es decir la regla de doblar la apuesta en cada lance) debería funcionar, en principio, pero en la práctica está expuesta a dos riesgos principales: la primera es la limitación del capital disponible. Como cada vez se duplica lo puesto, éste aumenta muy rápidamente, pero hemos visto que pueden aparecer largas secuencias de acontecimientos contrarios. Si tenemos la capacidad de apostar hasta n redoblamientos, podemos estar seguros de que tarde o temprano nos encontraremos con una secuencia adversa de longitud n+1. La segunda razón es social. Supongamos que hicimos 10 dobles a partir de 1 €, y por eso ahora estamos apostando 1024 €. Supongamos que ganamos. Nuestra victoria real es de 1 €, pero ¿cómo no ofrecer una bebida a todos los amigos cuando se gana 1 €? Siguiendo este método, ustedes se convertirán en impopulares muy pronto.
Ahora cambiamos un poco el juego. En lugar de apostar una moneda única, nos centramos en las secuencias de tres números. Hay ocho subsecuencias posibles: 000, 001, 010, 011, 100, 101, 110, 111. Podemos pensar en una ruleta en particular, donde en lugar de números usted apuesta a secuencias de números.
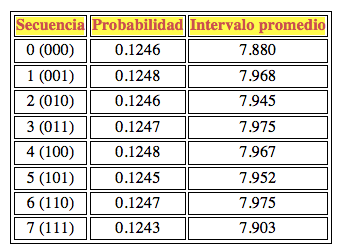
Obviamente, la probabilidad de que con tres lanzamientos de monedas encontramos una secuencia dada es la misma para cualquier secuencia. E, igualmente, si se tiene una secuencia de lanzamientos muy larga, se encuentra el mismo número de apariciones de las diversas subsecuencias. Como puede verse en el ejemplo (10000 repeticiones), la probabilidad de los intervalos entre dos apariciones es la misma para todas las secuencias.
Espero que en este momento usted está de acuerdo conmigo, porque ahora se empieza a jugar de veras. En primer lugar, vamos a estudiar el tiempo (promedio) de la primera aparición de las diversas secuencias. Es decir: usted elige una secuencia, por ejemplo 101, y, a continuación, se lanza una moneda hasta que no aparece esta secuencia, y luego grabamos el número de tiros necesario. Luego repetimos el experimento muchas veces. Todo el mundo (incluido yo) espera que, por lo que hemos dicho, el tiempo hasta la primera aparición de las distintas sub-secuencias es el mismo, pero no es así. Esto es lo que le sucede a unas secuencias.
Como se puede ver a simple vista, la secuencia de “000” aparece mucho después de la “011”! Y aquí están las estadísticas de 10000 logros.
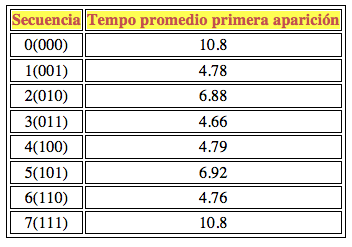
Increíble, ¿no? Las secuencias “000” y “111” aparecen mucho más tarde que las demás. Se puede ilustrar este fenómeno con secuencias de dos: por simetría “00” tiene el mismo tiempo medio de aparición de la secuencia “11” y “10” de “01”, por lo que sólo importa estudiar una pareja. Tomamos por ejemplo la secuencia 00, y la secuencia 10. Si el primer tiro dio “1” (50% de probabilidad), la secuencia “10” tarde o temprano va a salir y, definitivamente, se presentará antes de la secuencia “00”. Si se trata de un “0”, con un 50% de probabilidad saldrá otro “0” (y así gana “00”), pero con el otro 50% saldrá un 1, y tarde o temprano “10” va a ganar. Así que “10” tiene un 75% de probabilidades de salir antes de “00”.
Como puede verse, hay secuencias que aparecen antes y otras que aparecen después.
Inspirado por este resultado, podemos realmente poner un juego de azar. Se trata de apostar la secuencia que saldrá antes. Aquí el tablero, y se necesitan monedas para lanzarlas en orden.
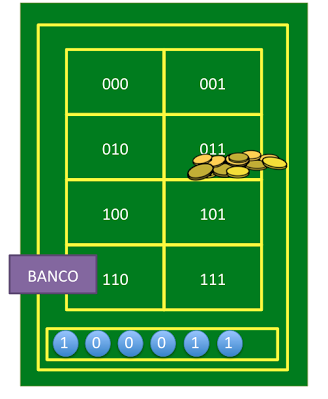
Por lo que hemos visto antes, nadie apostará en las secuencias más retrasadas “000” y “010”, y tampoco en las intermedias “010” y “101”, pero creo que todo el mundo está de acuerdo en que es indiferente apostar a cualquier otra. ¡Pero no! Si el segundo jugador conoce el truco, siempre puede (estadísticamente) ganar al primer jugador.
¿Cuál es el truco? Pongan 50 € en un sobre…
Ok, se los diré. Si el primer jugador juega una secuencia ABC, la secuencia bAB (donde b es lo contrario de B) sale estadísticamente antes. Así que para vencer, por ejemplo, “011” se debe apuntar a “001”. Esto se conoce como “el juego de Penney” [https://en.wikipedia.org/wiki/Penney’s_game] y es un ejemplo de juego no transitivo (como “Rock Paper Scissors”).
La línea está abierta, ¡hagan sus apuestas!
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
César ruiz -
Fabuloso.Para mi la clave es 10 y 01. Un saludo.