De giros en aviones y bicicletas

Ciencia

De giros en aviones y bicicletas

18 octubre, 2016
|
POR Rosa María Herrera
|
0 COMENTARIOS
|
Like 0
|
817

A Simon,
con más de 10 años de retraso…
(y a quienes como él sienten curiosidad y observan)

– Los aviones se inclinan para girar como las bicicletas.

Simon veía a través de la escotilla del avión, en nuestro vuelo Madrid-Frankfurt. No había llegado a los 7 años, pero sus dotes de observación me resultaban asombrosas; a mí que no soy experta en niños.

Intenté iniciar una conversación con la posibilidad que me brindó:

– Bueno, en realidad no basta sólo con inclinarse en la dirección de giro…

– Sí, ya sé, en mi bici también giro el manillar.

Me animé a seguir y dije:

– En realidad no es suficiente con girar el manillar e inclinarse. Imagínate que estuvieses con tu bicicleta en una pista de hielo, por mucho que girases el manillar no lograrías cambiar la dirección y posiblemente te acabarías dando un buen golpe sobre la pista.

– ¡Piensas que soy tonto!, nunca voy en bicicleta por la pista de patinaje, que para eso tengo patines…

Tras esta respuesta realista, la conversación “giró” a otro asunto de su interés. El tema ya estaba agotado…

De bicicletas y aviones

Para dar una curva con una bicicleta tienen que concurrir varias circunstancias simultáneamente: el giro del manillar, la inclinación de la bici, y el rozamiento del terreno. Así se consigue una presión asimétrica sobre la rueda que origina el empuje lateral necesario para producir el cambio de dirección.

El señor de la derecha, de aspecto simpático, pasea sonriente realizando de modo automático la maniobra oportuna para efectuar un pequeño giro, quizá conscientemente ajeno a la física de su movimiento. O tal vez no, porque todo es relativo… También podía estar pensando divertido sólo en la fotografía que le estaban tomando o en cualquier otra cosa.

En los aviones, el timón es el elemento con el que se realizan el tipo de maniobras equivalentes a las que se efectúan con el manillar en las bicicletas. El timón, que forma parte de los elementos de control de vuelo, se encuentra situado en la cola. Para realizar un viraje, el piloto regula la rotación a lo largo del eje vertical, accionando el timón. Simultáneamente, con un movimiento de los alerones, consistente en un descenso de un ala y un levantamiento de la otra, origina una rotación a lo largo del eje horizontal en la dirección del movimiento. Esto permite un posterior pequeño empujón asimétrico, útil para proporcionar la fuerza lateral que hace girar la aeronave.

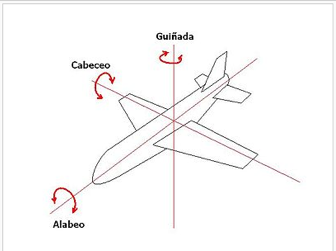
Figura 2. Principales ejes de rotación en un avión (Wikipedia)

La energía que se invierte en el viraje conlleva una ligera pérdida de altitud que se puede compensar durante el mismo viraje, aumentando levemente el ángulo de ataque [1] y aplicando una tercera rotación a lo largo del eje paralelo a las dos alas. Tres movimientos de giro que hábilmente combinados producen el resultado final de un único giro.

Las matemáticas y las rotaciones

Figura 3. Ejes de giro de los diferentes planetas del Sistema Solar

Las rotaciones, como las que realizan los planetas y otros cuerpos [2] del Sistema Solar en torno a su eje, o los aviones y la bicicletas para cambiar la dirección de su movimiento, se pueden trabajar matemáticamente a través de objetos matemáticos llamados matrices [3], mediante los cuales es posible operar ciertas transformaciones lineales [4]. Para cada transformación lineal existe una matriz asociada, y a cada matriz le corresponde una única transformación lineal.

En ese sentido, en la mecánica (y en otras ramas de la física), las matrices sirven para describir una amplia clase de transformaciones del espacio tridimensional en sí mismo. Por ejemplo, en las rotaciones y cambios de orientación que es lo que nos interesa en esta nota.

Veamos el procedimiento someramente: una posición espacial se determina mediante tres números o coordenadas. Cualquier sistema de coordenadas puede definirse fijando un origen, la terna (0, 0, 0) y los tres ejes de referencia, perpendiculares entre sí, X, Y, Z. De este modo, se establece una correspondencia unívoca entre ternas de números, x, y, z y los puntos del espacio.

La imagen de una matriz es la siguiente: una tabla de n x m elementos ordenados en filas (en horizontal), que se indican con el primer subíndice, y columnas (en vertical), que se marcan con el segundo subíndice. Si n = m la matriz se denomina cuadrada, en el caso del giro de los aviones necesitamos recurrir a matrices cuadradas 3 x 3 como la siguiente:

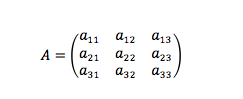
Éstas funcionan como una máquina que transforma tres coordenadas de un punto del espacio en otras tres. Digamos que alguien toma un vaso que está en el extremo de una mesa y lo pone en el centro. Eso se hace sin pensar mucho. Pero si el trabajo lo hiciera un robot, éste requeriría una transformación lineal, con una matriz de por medio.

Las matrices se pueden multiplicar siguiendo una regla sencilla (algoritmo de la multiplicación). Aquí nos interesa señalar que este producto no es conmutativo, concepto por demás valioso en la mecánica de giro.

También vamos a necesitar trabajar con otro tipo de matrices: las matrices fila y las matrices columna, que son las formadas respectivamente por una fila o una columna. Otra noción muy productiva es la de matriz traspuesta, M^T, que es la que resulta de cambiar en la matriz de partida las filas por columnas y viceversa. Así es que trasponiendo dos veces una matriz volvemos a la matriz primitiva.

Y ahora, con este bagaje, vamos a ver algunas definiciones de interés relacionadas con tales juguetes y sus reglas: una matriz es unitaria si al multiplicar su traspuesta por la matriz inicial se obtiene como resultado la matriz identidad, I, que es una matriz cuyos elementos son todo ceros excepto los de la diagonal principal [5], que son unos.

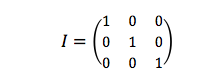
A su vez, la matriz identidad es unitaria, y se verifica que I^T = I y que I^T ^.I = I.

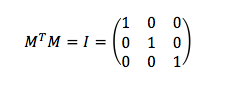
La matriz identidad no produce ninguna modificación espacial. Lo que es lo mismo que decir que el producto de una matriz unitaria M por su traspuesta M^T deja el espacio inalterado.

La mayor parte de las matrices unitarias representan rotaciones, una vuelta al origen, y así volvemos a enlazar el punto de partida con los aviones, bicicletas y planetas girando alrededor de un eje de rotación.

Poniendo a funcionar nuestro cerebro en modo matemático podemos decir, más o menos formalmente, que un eje de rotación es un conjunto de puntos (x, y, z) cuyas coordenadas permanecen invariables mientras se realiza el movimiento de giro. Y aquí usamos la idea de matriz columna y el algoritmo del producto de matrices [6]. Las coordenadas (x, y, z) en cada rotación cumplen, pues, la siguiente condición:

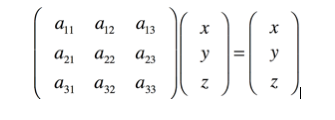
Por otra parte, las rotaciones del espacio respecto a un eje que pasa por el origen producen matrices unitarias.

Un ejemplo es el siguiente:

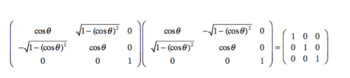
La primera matriz de este producto representa una rotación alrededor del eje Z. El ángulo ha girado en sentido antihorario (en el caso en que no se produce ningún giro). Giros análogos con respecto al eje Y y al eje X, se representan por matrices similares a éstas.

De hecho, una de las propiedades de las matrices unitarias es que modifican los puntos del espacio dejando invariante su distancia recíproca. Unos ojos curiosos que observan con interés el movimiento en torno a un eje de un objeto que sirve para cambiar su orientación (pero nada más), quedan muy complacidos con esta herramienta matemática.

Una brevísima digresión sobre distancias que no cambian en los movimientos…

Intuitivamente tenemos una idea eficaz de distancia (incluso muchas veces también en el sentido más poético y emocional), pero ¿cómo manipular esa intuición para que resulte un concepto útil? Como tantas veces en física, usamos la idea matemática –en este caso geométrica- como herramienta. Evidentemente descartamos las modificaciones (movimientos) de los objetos que suponen deformaciones físicas, cambios de estado o, en general, otras transformaciones de la estructura del objeto.

Además de las rotaciones en torno a un eje que acabamos de describir, también una combinación de rotaciones es una herramienta interesante. Multiplicando repetidamente las matrices de giro, se pueden conseguir otros giros respecto a ejes que pasan por el origen, que no coinciden con ninguno de los 3 ejes X, Y, Z.

Visualmente se aprecia que las traslaciones no alteran el aspecto y la estructura del cuerpo. Y además también las reflexiones [7] respecto a un plano, que transforman un objeto en su imagen especular, mediante un mapeo (dejan invariantes las distancias). Pero esto queda fuera del propósito de la presente nota.

Producir movimientos a distancia

Acabo con un comentario breve para tratar de provocar curiosidad e interés. Otros ejemplos donde es útil el trabajo con las matrices para producir movimientos son los siguientes: en los satélites que se orientan a decenas de miles de kilómetros mediante órdenes de radio enviadas desde la Tierra; en los videojuegos en los que hay cambios de situación mediante joysticks. Cuando hay cambios de dirección, la estructura laberíntica que se esconde en la memoria del ordenador no se altera físicamente, pero el aspecto que percibimos en nuestra visión del juego en la pantalla varía. Los cambios de orientación visuales se diseñan usando matrices que expresan dichas modificaciones. C²

Referencias

Ángulo formado por la cuerda (geométrica) del ala y la dirección del viento.
El movimiento de traslación de los cuerpos naturales del sistema es un movimiento periódico (de giro alrededor del Sol caso de los planetas, asteroides, etc. o alrededor de un planeta caso de satélites), pero no lo consideramos aquí.
Las matrices son tablas de números que cumplen ciertas propiedades.
Transformación lineal es una función que convierte un espacio vectorial en otro.
Diagonal principal en una matriz 3 x 3 es la que contiene los elementos a₁₁, a₂₂, a_33.
El algoritmo de la multiplicación de matrices se puede encontrar en Wikipedia https://es.wikipedia.org/wiki/Matriz_(matem%C3%A1ticas) y en general en lugares adecuados de la red.
En general los movimientos que dejan geométricamente invariable un objeto se denominan isometrías.

Bibliografía

[1] MILANI, A. & GRONCHI, C.: Theory of the orbit determination. Cambridge University Press, 2010

[2] Minute of physics https://www.youtube.com/watch?v=iWSu6U0Ujs8

[3] MOSER, J.K.: Stable and Random Motions in Dynamical Systems. Princenton Landarmarks in Mathematics

[4] WAGENSBERG, J. (ed.): Sobre la imaginación científica, (Qué es, cómo nace y cómo triunfa una idea). Metatemas, Tusquets editores, Barcelona, 1990

Sobre el autor

Rosa María Herrera

Profesora e Investigadora en UPM, España

Estudió física. Su interés es sobre la estabilidad dinámica del Sistema Solar y los sistemas hamiltonianos de baja dimensión. Se interesa además por los principios variacionales en física y la divulgación científica.