Más que detallar el caso de los polígonos regulares, en esta nota hablaremos del caso general del área de un polígono (sea o no regular).
En particular detallaremos el caso de un polígono en un plano discreto (las coordenadas son valores enteros), y el caso general donde el plano es un plano real (las coordenadas son valores continuos).
El cálculo de áreas es un tema harto conocido en el caso de un polígono regular (uno en el que sus lados son del mismo tamaño) y es simplemente:
área= perímetro × apotema/2
El perímetro es directamente el número de lados multiplicado por el tamaño de un lado, y el apotema es la distancia del centro del polígono al centro de uno de sus lados.
El caso discreto
El austriaco Georg Pick es conocido por dos notables hechos: a) Haber sido clave para que el joven Albert Einstein ingresara a la Universidad de Praga en 1911; y b) Publicar un artículo sobre geometría reticular (plano discreto) en el que presentó una fórmula para el cálculo de un polígono, cuando los vértices del mismo están ubicados en los puntos de cruce de la retícula, conocido como el Teorema de Pick.
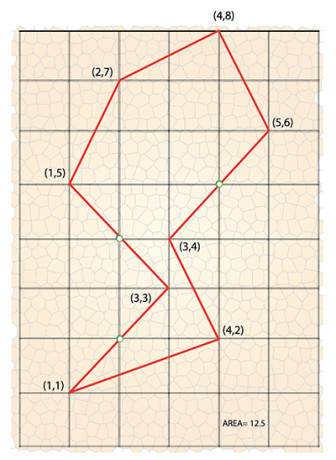
Para entrar en materia, nos referiremos a la figura 1 en la cual en color rojo se muestran los puntos externos del polígono (correspondientes a los vértices o que están en el perímetro) y en color azul se indican los puntos internos del polígono. Sorprendentemente el área del polígono es simplemente:
área= número puntos externos /2 + número puntos internos – 1
Para la figura 1, tenemos un total de 11 puntos externos y 8 puntos internos, de modo que el área total es (asumiendo que la retícula tiene divisiones en metros):
área= 11/2 +8 – 1 = 12.5 m2
Es importante hacer notar que el área de un polígono es invariante a su localización dentro de una retícula (plano discreto).
La única limitante del Teorema de Pick es que no se puede utilizar cuando los vértices están ubicados en un plano continuo (los vértices no coinciden con los elementos de la retícula).
El caso continuo
No es tan simple como el Teorema de Pick. En este caso el área se puede conocer cuando las coordenadas de los vértices son conocidas. Tomemos como ejemplo el mismo caso de la figura 1, no obstante, ahora consideremos solo las coordenadas de los vértices (ver figura 2).
Empezando en cualquier vértice y recorriendo el polígono en cualquier sentido, se designa al primer vértice con sus coordenadas (x1, y1), al segundo con (x2, y2) y el último (asumiendo n lados) (xn, yn), y se calcula el área con la fórmula:
área= (x1*y2 –x2*y1 + x2*y3 –x3*y2 +…+ xn*y1 –x1*yn)/2
Aun cuando esta fórmula es difícil de recordar, hay una manera de realizar el cálculo, y este consiste en yuxtaponer verticalmente las coordenadas repitiendo, al final, la primera coordenada; luego se debe multiplicar en cruz las coordenadas consecutivas. Las multiplicaciones de izquierda a derecha conservan su signo, y las de derecha a izquierda se les cambia el signo; se suman y se dividen entre 2. Para ejemplificar el cálculo, tomemos las coordenadas de la figura 2.
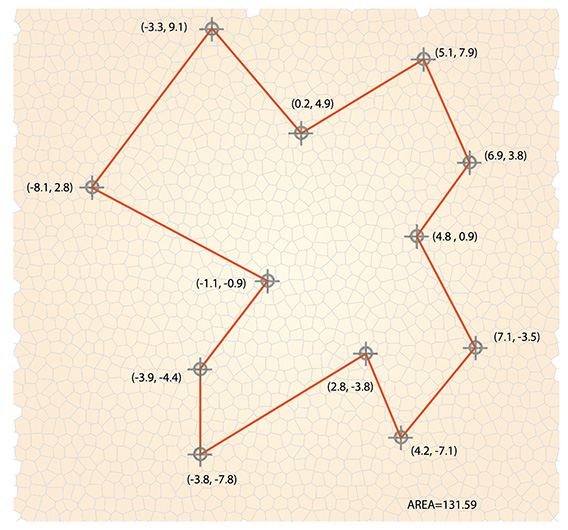
Un ejemplo que ilustra las bondades
de este segundo método se presenta
usando la Figura 2
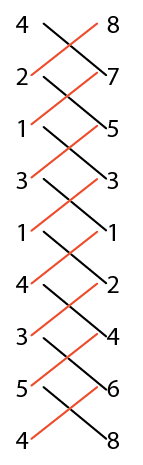
área= (4*7-8*2+2*5-7*1+1*3-5*3+3*1-3*1+1*2-1*4+4*4-2*3+3*6-4*5+5*8-6*4)/2=12.5

