El problema de los cuatro colores ha sido durante mucho tiempo una pesadilla en matemáticas. Se trata de probar que sólo con cuatro colores se puede pintar un mapa trazado en un plano o en una esfera, de tal modo que las regiones que compartan al menos una frontera no sean del mismo color.
Fue planteado por primera vez en 1852 por Francis Guthrie, mientras coloreaba un mapa de Inglaterra. La prueba aceptada hasta ahora fue formulada en 1976 por Wolfgang Haken y Kenneth Appel en la Universidad de Illinois, con la ayuda de una computadora.
Ésta es la historia
En 1852 Francis Guthrie, estudiante graduado del Colegio Universitario de Londres, quien se dedicaba a elaborar mapas, se dio cuenta que al parecer eran suficientes cuatro colores para pintar los mapas de tal modo que las regiones que tuvieran una frontera en común fueran de colores distintos (Guthrie,1880). Francis le comunicó dicha observación a su hermano menor Frederick, quien a su vez se la hizo saber a su profesor. El primer documento conocido que habla acerca del problema de los cuatro colores es una carta con fecha del 23 de octubre de 1852, escrita por Augustus DeMorgan a su colega y amigo Sir William Rowan Hamilton. En ella decía que su estudiante Frederick Guthrie le había planteado un problema y no había sido capaz de resolverlo.
El problema fue olvidado hasta 1878, cuando Arthur Cayley lo mencionó en los Proceedings of the London Mathematical Society invitando a que fuera resuelto. En 1879 Alfred B. Kempe anunció una prueba para la conjetura de los cuatro colores. Esta prueba fue aceptada durante once años, hasta que en 1890 Percy J. Heawood demostró que existía un error en ella. Sin embargo, Heawood no consideró completamente erróneo el trabajo de Kempe, pues utilizó sus bases para desarrollar la primera prueba del teorema de los cinco colores (Heawood, 1890).
Un grafo es un conjunto de vértices o nodos unidos por aristas o arcos, que representan relaciones binarias.
En 1880 Peter G. Tait también publicó una prueba la cual se vio que no era correcta. Para entender el error de Tait debemos saber que un grafo es un conjunto de vértices o nodos unidos por aristas o arcos, que representan relaciones binarias entre elementos de un conjunto; cuando este grafo contiene un ciclo de Halmilton se denomina Halmiltoniano. Un ciclo simple en un grafo G se dice que es de Halmilton si contiene todos los vértices de G (González, 2004). Tait basó su prueba en el falso supuesto de que todo grafo plano tres-conectado es Hamiltoniano, lo cual resultó una prueba no válida (Saaty y Kainen, 1986).
El problema de los cuatro colores siguió causando un gran interés en la comunidad matemática. Una vez que se tuvo la prueba de Heawood para el teorema de los cinco colores, las investigaciones fueron enfocadas en la reducción de los colores necesarios para la coloración de mapas y grafos. Muchos de los planteamientos que originalmente fueron desarrollados para resolver este problema se convirtieron en parte fundamental del conocimiento matemático, un ejemplo claro de esto es el surgimiento de la teoría de grafos, dentro de la cual una parte importante es la coloración de grafos, originada con la idea de Francis Guthrie.
Philip Franklin demostró que todos los mapas de 25 o menos regiones cumplen con la conjetura de los cuatro colores.
En 1922 Philip Franklin demostró que todos los mapas de 25 o menos regiones cumplen con la conjetura de los cuatro colores (Franklin, 1922). Posteriormente, los siguientes autores, y el mismo Franklin, demostraron lo mismo pero para un mayor número de regiones: C. N. Reynolds en 1926, 27 regiones; Philip Franklin en 1938, 31 regiones; C. E. Winn en 1940, 35 regiones; Oystein Ore y Joel Stemple en 1968, 40 regiones (Ringel, 1974; Saaty y Kainen, 1986). Estas demostraciones nos indican el número de regiones que debiera tener un contra-ejemplo para la conjetura de los cuatro colores. Por ejemplo, de acuerdo a Ore y Stemple, si existiera este contra-ejemplo debería ser en un mapa con al menos 41 regiones.
En 1931 Whitney introdujo el concepto de gráfico dual (Whitney, 1931), utilizándolo para dar una elegante caracterización a los gráficos o mapas planos (Saaty y Kainen, 1986).
En 1936 König publica el primer libro sobre teoría de grafos. En 1941 R. L. Brooks anuncia su teorema, el cual da un salto en el número cromático de cualquier grafo (Brooks, 1941); el número cromático, χ (G), es el menor número de colores necesarios para colorear un grafo G. Posteriormente en 1943 H. Hadwiger publica una conjetura, donde el problema de los cuatro colores forma parte de ella como un caso especial (Saaty y Kainen, 1986).
Continuando con el interés en este tema, en 1952 Dynkin y Uspenski escriben un pequeño libro de ejercicios de coloración; Gerhard Ringel también publica dos libros de coloración de grafos, uno en 1959 y otro en 1974. Oystein Ore escribe tres importantes libros acerca de este tema: Theory of graphs (1962), Graphs and their uses (1963) y The four-color problem (1967).
Mientras tanto el número de regiones que deben de tener los mapas para cumplir con la conjetura de los cuatro colores se incrementó a 52 y posteriormente a 96 (Saaty y Kainen, 1986).
En una fecha más reciente se comprobó esta prueba, utilizando también una computadora.
Finalmente, en 1976, Kenneth Appel y Wolfgang Haken obtienen la última prueba aceptada hasta ahora para la conjetura de los cuatro colores (Appel y Haken, 1976). Esta prueba la realizaron con ayuda de una computadora; el gran número de operaciones necesarias para la demostración, el extenso tiempo (1200 horas) que se tomó en realizar los cálculos, así como la imposibilidad para una persona de verificar la prueba manualmente, generó una polémica que se mantiene hasta ahora acerca de la veracidad de esta demostración (Saaty y Kainen, 1986). En una fecha más reciente se comprobó esta prueba, utilizando también una computadora. Aún así no es aceptada por todos los matemáticos, tanto por la controversia de si las pruebas elaboradas con cálculos extensos por computadoras deben considerarse válidas, como por ser poco elegante, según alegan algunos científicos. Se dice que cuando la prueba fue publicada alguien dijo: “Una buena prueba matemática es similar a un poema, ¡pero esto es una guía telefónica!”
El problema de los cuatro colores ha resultado muy interesante desde que fue planteado.
El problema de los cuatro colores ha resultado muy interesante desde que fue planteado. Como otros muchos problemas en matemáticas, se ha intentado resolver de varias formas y ha estado rodeado de pruebas que después se encontraron falsas. Sin embargo, no por ello la investigación que se generó fue en vano. De hecho, aportaron conocimientos a otras cuestiones en las matemáticas y abrieron nuevos campos de estudio. Finalmente, con la ayuda de la computación la prueba pudo ser realizada, siendo el primer teorema demostrado con la ayuda de una computadora. Esta prueba ha provocado una gran controversia, pues aunque existen distintas opiniones acerca del uso de las computadoras para la elaboración de pruebas matemáticas, prevalece la polémica pregunta: ¿podemos aceptar como cierta una afirmación que sólo una máquina, y no una mente humana, puede comprobar?
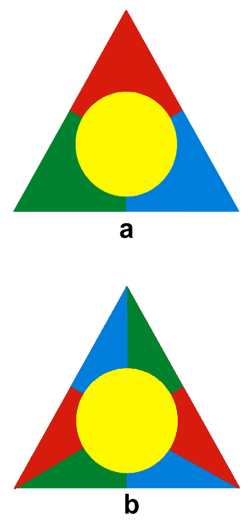
En estos mapas (Figura 1) se observa claramente la necesidad de cuatro colores como mínimo para que ninguna de las regiones adyacentes comparta el mismo color.
En el mapa a existen cuatro regiones mutuamente adyacentes, por lo que hay una obstrucción local para un mapa 3-coloreable, es decir, posible de colorear con tres colores, la necesidad de cuatro colores resulta obvia. El mapa b ilustra una para un mapa 3-coloreable; esto es, si se omite por un momento la región central y el resto del mapa es coloreado con tres colores, entonces para colorear el centro se necesita un cuarto color (Saaty y Kainen, 1986). C2
Referencias
- Akiyama, J. y Hamada, T. (1980). Another proof of five color theorem. Bul. Liber. Arts & Science. NMS. Vol. 1
- Appel, K. y Haken, W. (1976). Every planar map is four colorable. Bull. Am. Math. Soc. Vol. 82.
- Birkhoff, G. D. (1913). The reducibility of maps. Am. Journal Math. Vol. 35.
- Brooks, R. L. (1941). On colouring the nodes of a network. Proc. Cambridge Philos. Soc. Vol. 37.
- Cayley, A. (1878). On the colouring of maps. Proceedings of the London Mathematical Society. Vol. 9.
- Franklin, P. (1922). The four color problem. Amer. J. Math. Vol. 44.
- González Gutiérrez, F. J. (2004). Apuntes de Matemática Discreta. Universidad de Cádiz. Escuela Superior de Ingeniería. Departamento de Matemáticas.
- Guthrie, F. (1880). Note on the coloring of maps. Proc. Roy. Soc. Edinburgh. Vol. 10.
- Heawood, P. J. (1890). Map colour theorem. Quart. J. Math. Vol. 24.
- Heesch, H. (1969). Untersuchungen zum vierfarbenproblem. B.I. Hochschulskripten, 810/810a/810b. Mannheim – Vienna – Zürich: Bibliographische Institute. (Los estudios sobre el problema de los cuatro colores-. B.I. Guiones altos, 810/810a/810b. Mannheim – Viena – Zurich: Instituto Bibliográfico.)
- Kempe, A. B. (1879). On the geographical problem of the four colours. Amer. J. Math. Vol. 2.
- Kempe, A. B. (1880). How to colour a map with four colours. Nature. Vol. 21.
- Ringel, G. (1974). Map color theorem. Springer-Verlag. Berlin Heidelberg New York.
- Robertson, N.; Sanders, D. P.; Seymour, P; Thomas, R. (1996). A new proof of the four-colour theorem, Electronic Announcements of the AMS. Vol. 2.
- Saaty, T. L. y Kainen, P. C. (1986). The four-color problem: assaults and conquest. Dover Publications, Inc. New York.
- Tait, P. G. (1880). Remarks on the colouring of maps. Proc. Roy. Soc. Edinburgh. Vol. 10.
- Whitney, H. (1931). A theorem on graphs. An. Math. Vol. 32.


Humberto Ceballos Gallardo -
Hola, la saludo desde el estado de Baja California donde actualmente estoy realizando mis estudios de maestría en la UABC. En mi búsqueda de información encontré una investigación en proceso realizada por usted llamada “Vivienda bioclimática sustentable en regiones de clima cálido árido: implicaciones ambientales, económicas y sociales” y me gustaría compartir impresiones con usted al respecto, ya que ahora mismo yo me encuentro trabajando en un proyecto similar.