Entrevista Imposible a Arquímedes. Uno de los más grandes matemáticos de la antigüedad.

Ciencia

Entrevista imposible a Arquímedes

13 febrero, 2018
|
POR Franco Bagnoli
|
1 COMENTARIOS
|
Like 0
|
939

FB (Franco Bagnoli): Para la entrevista imposible de hoy tenemos aquí a Arquímedes de Siracusa. ¡Buenos días, maestro!

AS (Arquímedes de Siracusa): Buenos días a usted y a todos los radioyentes.

FB: Creo que todo el mundo ha oído hablar de usted, pero tal vez no todos recuerden exactamente el tiempo en el que vivió. ¿Podría refrescarnos la memoria?

AS: Nací en Siracusa, la ciudad más grande de Grecia, en el año 287 antes de Cristo.

FB: Pero, ¿Siracusa no está en Sicilia, Italia?

AS: Exactamente, la Magna Grecia, así llamada porque sus ciudades fueron más suntuosas que las de la Grecia clásica. Morí allá en el 212, a manos de un soldado romano, cuando Siracusa fue conquistada, después de tres años de asedio, por el general Marcelo. Ese general me honró con una suntuosa tumba, coronada por una esfera y un cilindro. Mi tumba fue redescubierta por Cicerón en 75 A.C., pero luego se perdió. Lo que hoy es mi tumba no es más que un sepulcro romano.

FB: ¿Puede decirnos cuáles de sus contribuciones a la ciencia le gusta recordar?

Figura 1. Arquímedes pensativo. Óleo sobre tela del pintor Domenico Fetti (1620).

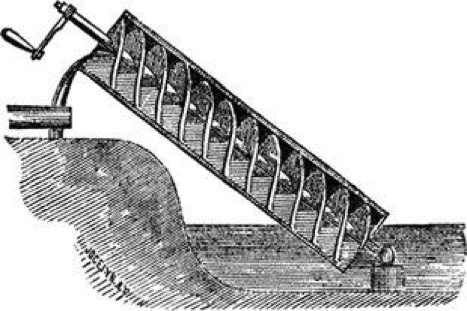
AS: Mmm, déjame pensar (Figura 1)… Soy considerado uno de los más grandes matemáticos de la antigüedad, pero en realidad, si tendrías que catalogarme de acuerdo a sus criterios modernos, yo diría que era más físico que matemático. Entre los descubrimientos que recuerdo con más placer están la bomba donde el líquido se sube mediante un tornillo (Figura 2), por lo que podemos decir que el fluido se eleva cayendo continuamente. Y luego, por supuesto, mis trabajos sobre hidrostática, de donde sale el principio de que lleva mi nombre, y mis investigaciones respecto a la palanca. Siempre he tratado de considerar problemas prácticos, por ejemplo, mis estudios sobre la palanca me han servido tanto para levantar las naves pesadas, como para construir catapultas y escorpiones, que son una especie de ballestas.

FB: Los siracusanos pudieron oponerse tanto tiempo a los romanos gracias a sus máquinas, ¿verdad?

AS: Sí, y si nuestros soldados no hubieran sido tan tontos como para emborracharse, Siracusa seguiría siendo independiente y tal vez nuestros aliados cartagineses habrían ganado las guerras púnicas. La técnica de ataque de una ciudad fortificada como Siracusa requiere de un progreso lento, paso a paso, utilizando pasarelas para superar las zanjas y escaleras para subir los muros, siempre protegiéndose con escudos o paredes móviles. Así que era esencial identificar los “puntos ciegos”, donde las catapultas no llegaban, con el fin de montar ahí las máquinas de asedio. En el caso de Siracusa, se tenía que comenzar por los buques. Pero mis máquinas estaban hechas de tal manera que se podía variar sus tiros, por lo que no había puntos ciegos. Además, nuestros soldados podían dejar caer mazos y piedras sobre los buques a través de palancas largas, o incluso levantar las proas de los buques usando una especie de manos prensiles o garras para hundirlos (Figura 3).

FB: E incluso quemó los barcos a distancia utilizando espejos.

AS: Eso de espejos ardientes es un mito nacido en la Edad Media. Mis máquinas podían, por supuesto, tirar sustancias incendiarias, para quemar las naves que nos tenían sitiados.

FB: Pero también es recordado por muchos trabajos matemáticos.

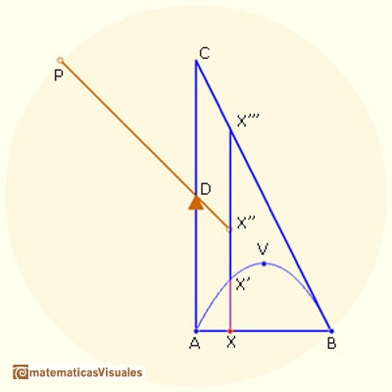
AS: Sí, por supuesto, en particular por el cálculo de la superficie del segmento parabólico, la relación entre el volumen del cilindro y la esfera, y por una aproximación del área del círculo. Pero incluso en este caso he usado métodos más físicos que matemáticos, en particular, utilizando la palanca (Figura 4).

Figura 4. El uso de la palanca para medir la area de un segmento de parábola. Imagen en http://www.matematicasvisuales.com/html/historia/archimedes/parabola.html — Figura 4. El uso de la palanca para medir la área de un segmento de parábola. Imagen en http://www.matematicasvisuales.com/html/historia/archimedes/parabola.html

FB: ¿En qué sentido?

AS: Me imaginaba recortar mi figura de una tabla de madera y ponerla sobre el brazo de una palanca, y luego poner en el otro brazo figuras equivalentes, con el fin de equilibrar el peso. De esta manera, podía estimar el área de la figura. Y teniendo en cuenta que se trataba de formas curvas, y ya que sabía calcular las áreas de los triángulos que tienen lados rectos, tenía que añadir más y más pequeños triángulos.

FB: Prácticamente, usted ha tenido que sumar un número infinito de términos …

AS: De hecho, y puedo decirlo sin falso orgullo, tal vez he utilizado por primera vez el hecho que una serie infinita de términos infinitesimales puede dar un resultado definido, un concepto muy difícil para nosotros, los griegos, que siempre hemos luchado contra paradojas como la de Aquiles. Esto funciona especialmente bien para la parábola, dando una serie geométrica que se puede sumar fácilmente.

FB: ¿Y el círculo?

AS: En este caso no he podido sumar la serie, ya que habría dado lugar a un número trascendental, que nosotros no conocimos. Pero llegué a aproximar el círculo con un polígono de 96 lados, que es prácticamente indistinguible en el sentido práctico. En términos modernos, he encontrado que pi está entre 3 + 10/71 y 3 + 1/7, o sea que su valor decimal está entre 3,1408 y 3,1428. Mis obras fueron leídas y estudiadas por Leonardo da Vinci, Galileo y Newton y quizás han inspirado a este último la idea del cálculo diferencial.

FB: Se dice que usted era también un gran bromista…

AS: No lo niego. En esos días había una intensa correspondencia entre algunos sabios, a pesar de que estábamos dispersos en varias ciudades del Mediterráneo, y me divertía enviando a mis compañeros unos desafíos que son casi imposibles de resolver, tales como el número de granos de arena que podía tener el universo o la cantidad de ganado que compone los rebaños de Helios, el Sol. ¿Se acuerda usted?, el ganado que se comieron los compañeros de Ulises, terminando muy mal. Entre otras cosas, la isla del Sol era, obviamente, mi Sicilia, y la historia tenía un sentido educacional: nunca desafiar Trinacria…

Figura 5. Las vacas de Helios, Homero, Odisea, libro X. Ulises, tras la profecía de Tiresias, había dicho a sus compañeros: “os lo ruego: respetas el ganado que hay en la isla. No lo toquéis bajo ningún concepto. No olvidéis nunca que su dueño es el Sol, el ojo y el oído del universo. El que todo lo ve y todo lo oye”.

FB: ¿Y cuál era la dificultad fundamental de estos problemas?

AS: Sus soluciones siempre requerían números muy grandes, que por supuesto tampoco se podían representar con los sistemas notacionales de mi época. Prácticamente se necesitaba la notación exponencial, algo, que a mi conocimiento, incluso en estos días no es muy común.

FB: ¿Puede dar nos un ejemplo?

AS: Tomemos el problema del rebaño de reses. Yo desafié a Eratóstenes (el de la famosa criba) para encontrar una solución a un problema formulado con una serie de limitaciones: había toros de cuatro colores, blancos, negros, oscuros y manchados, y vacas de muchos tipos. Entonces dije que el número de toros blancos era la mitad más un tercio de los negros más los oscuros, el número de vacas blancas era igual a un tercio, más una cuarta parte de la suma de todos los animales negros, y así sucesivamente con otras condiciones para un total de siete ecuaciones lineales con ocho incógnitas, que pueden ser reducidos a la solución de una ecuación cuadrática, pero con coeficientes muy grandes. Obviamente había que utilizar sólo números enteros para no matar a ningún animal, cosa que hubiera suscitado la ira del Sol como con los compañeros de Ulises. El resultado es de unos cincuenta millones de cabezas. Pero entonces añadí que aquellos que lo había resuelto no eran todavía sabios, ya que había aún dos condiciones cuadráticas, a saber, que la suma de los toros blancos y negros tenía que ser un número cuadrado, tal como 4, 9, 16, y que la suma de los toros oscuros y los manchados tenía que ser un número triangular, tal como 3, 6, 9 (los números triangulares son dados por la suma de los primeros números enteros). Me ha llegado el rumor de que en 1880 dos matemáticos alemanes, Krumbiegel y Amthor, resolvieron el problema y encontraron que la solución mínima es alrededor de 10 a la 200.000, o sea usaron los exponenciales, que era entonces lo que quería.

FB: ¿Pero usted lo había resuelto?

AS: Bueno, ya saben cual es mi expresión más famosa: ¡Eureka!, Que significa “lo he encontrado”.

FB: Sí, todos la usamos ahora. Muchas gracias, profesor.

AS: Fue un placer. No los invito a venir a visitarme, por razones obvias. Pero si se le ocurre pasar por el limbo, no deje de darme un saludo. Y lean El código de Arquímedes de William Noel y Reviel Netz, para descubrir más cosas de mí.

(Esta entrevista imposible se realizó por RadioMoka, transmisión en NovaRadio http://www.caffescienza.it/radiomoka)

Sobre el autor

Franco Bagnoli

Departamento de Física y Astronomía en Universidad de Florencia (Italia) | Website

Estudió física. Enseña física de sistemas complejos y física computacional. Su investigación es sobre sistemas complejos, ciencia cognitiva, psicología, biología y evolución. Es presidente de la asociación de divulgación científica Caffè-Scienza Firenze www.caffescienza.it