Como homenaje al 40 aniversario del cuento de Carl Barks “Perdidos en el Andes” [1], Don Rosa produjo una secuela titulada, “Regreso a Cuadrolandia” [2], ver figura 1.

En este cómic, Donald y sus sobrinos tienen que competir contra Gilberto Oro (Flintheart Glomgold) para entregar un helado “con refresco” (ice cream soda [3]) al presidente de Cuadrolandia (Plain Awful) y rescatar a su tío Rico MacPato, detenido por “hacer formas redondas”. En Cuadrolandia todo es cuadrado y hacer cosas redondas constituye un crimen inimaginable. MacPato, pretendiendo inculcar el amor al dinero a los ingenuos cuadrolanderos, muestra su primera moneda y termina condenado a trabajos forzados. Gilberto, por supuesto, traiciona el acuerdo previamente establecido tras haber conseguido el helado, lo que obliga a los chicos a fabricar un refresco helado de emergencia allí mismo, utilizando leche en polvo, azúcar y chocolate de sus raciones de comida, congelando los ingredientes mezclando sal y nieve, y finalmente reemplazando el refresco con el agua carbonatada de un extintor de incendios.

Este relato puede servir como introducción al hecho “misterioso” de que añadir sal derrite el hielo [a], pero este fenómeno se acompaña con la reducción de la temperatura de la mezcla [4]. Es evidente que, para un espectáculo de física, elaborar instantáneamente (mejor dicho, bastante rápidamente, pues se necesita una media hora) helado para distribuirlo al público es una manera fácil de conseguir su atención [5].
El fenómeno presentado no se puede explicar de manera sencilla porque no podemos basarnos simplemente en consideraciones energéticas. De hecho, las moléculas de agua y los iones de sal (sodio y cloro) “prefieren” permanecer separados desde el punto de vista energético y sabemos que lo hacen por debajo de -21 ºC (por lo tanto, es inútil regar sal en las calles heladas a temperaturas inferiores a ésta).
¿Qué sucederá por encima de este valor de la temperatura? Sabemos que se producen transiciones de fase (por ejemplo, hielo-agua) con absorción de calor sin cambio de temperatura (calor latente), pero la situación que presentamos parece ser diferente. Podemos ver el problema con el modelo “Mercedes-Benz” [6] que también utilizamos para ilustrar la disminución de la densidad del agua durante la congelación [7].

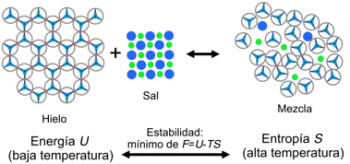
Como puede verse en la Figura 3, los iones de cloro y de sodio (ambos cargados) se acoplan bien con las moléculas de agua, que son polares, pero al hacerlo interrumpen la estructura ordenada de los cristales de hielo y sal. Como para la fusión, este hecho implica que la mezcla es estable a altas temperaturas, y que los cristales son estables a bajas temperaturas.
Entonces, ¿por qué la temperatura disminuye cuando la sal se mezcla con el hielo? Volvamos a la explicación anterior: estructuras desordenadas son estables a altas temperaturas, y estructuras ordenadas lo son a bajas temperaturas. Estas últimas están claramente favorecidas por la energía, pero ¿qué ocurre con las primeras? Para entenderlo bien es conveniente introducir el concepto de entropía S, que es el (logaritmo del) número de configuraciones posibles.
Utilizando un modelo simple unidimensional (Fig. 4), podemos apreciar la diferencia en el número de configuraciones para estructuras ordenadas y desordenadas. Si la diferencia de energía entre los dos tipos de estructuras es grande, se prefiere el orden con fluctuaciones ocasionales y locales (para temperaturas por encima del cero absoluto y en un marco clásico). Pero si la diferencia de energía no es muy grande, las fluctuaciones que elevan la energía tienen lugar con mayor frecuencia, y cuando el orden se destruye, se recupera con dificultad porque hay muchas configuraciones desordenadas próximas, no muy lejanas energéticamente, y solo una ordenada.
Los científicos acostumbran a introducir el concepto de energía libre F = U – TS, donde U es la energía y T la temperatura. La estabilidad de un sistema está dada por el mínimo de la F, y de la fórmula anterior es fácil ver que la temperatura, si es baja, hace que prevalezca el término de la energía, y la entropía (que tiene signo menos) cuando es alta.
Se puede ilustrar experimentalmente el problema con una huevera de cartón (Fig. 5) y unas cuantas bolitas. Las abolladuras [b]de la huevera representan los mínimos de la energía.

Ponemos todas la bolitas en una abolladura y agitamos ligeramente la huevera para simular la temperatura. A bajas temperaturas las bolitas permanecen en la abolladura original, y a temperaturas más altas saltan por todas partes. Pero, aun a baja temperatura, ocasionalmente algunas bolitas saldrán de su hueco, y probablemente al cambiar nuevamente de abolladura no volverán a la anterior, sino que continuarán saltando de unas a otras. En realidad, este modelo no es perfecto: las moléculas en el hielo y en la sal se atraen recíprocamente. Un modelo más realista debería usar esferas imantadas con magnetización muy débil. En este caso, la agitación térmica lograría separar las esferas que tenderían a reunirse de nuevo, porque la configuración reagrupada corresponde a un mínimo de la energía. Si se vuelven a agitar, de una manera suficientemente enérgica, es posible separar las esferas (siempre y cuando la atracción entre ellas no sea demasiado fuerte), y las esferas permanecerán separadas a pesar de la energía (fuerza de atracción) debido a que la entropía es superior a causa de la temperatura.
Parte de la energía transmitida en la agitación sirvió para separar las esferas; en el mundo ideal (conservativo) de las moléculas, esto se corresponde con un descenso notable de la temperatura (en nuestro mundo disipativo, toda la energía al final se convierte en calor, y por eso hay que comunicar continuamente energía al sistema).
Así, añadiendo sal al hielo por encima de -21 ºC, las moléculas tienden a alcanzar una configuración estable mediante la mezcla, pero este proceso requiere aporte energético para romper los enlaces de hidrógeno de hielo y para disolver la sal (el calor latente de hielo es 6,01 kJ/mol y el del cloruro de sodio 3,87 kJ/mol).
Y ahora nuestro desafío: ¿por qué la escala Fahrenheit es tan extraña y por qué se corresponde su cero a (aproximadamente) -18 ºC? [c]C2
Referencias:
[a] de hecho en invierno se suele echar sal sobre las carreteras heladas
[b] huecos u orificios donde se depositan los huevos
[c] En la época de Daniel Gabriel Fahrenheit (1686-1736), la mezcla de sal, hielo y agua caracterizaba la temperatura más baja que se puede obtener fácilmente y sin herramientas de laboratorio, y se utilizó para definir el cero de la escala Fahrenheit (usando volúmenes iguales de hielo y sal ), mientras que 100 grados Fahrenheit corresponden (más o menos) a la temperatura del cuerpo [8], otra temperatura fácil de conseguir. Las ventajas de esta escala es que no necesita temperaturas negativas en la vida cotidiana, y (con la actual escala refinada) hay una separación de 180 grados entre el punto de ebullición y el punto de congelación del agua, lo que hace más fácil expresar temperaturas sin necesitar decimales.
[1] BARKS, Carl. Lost in the Andes!, http://coa.inducks.org/story.php?c=W+OS++223-02 , http://en.wikipedia.org/wiki/Lost_in_the_Andes! (1949). Para leerlo online:
[2] ROSA, Don. Return to plain awful, http://coa.inducks.org/story.php?c=AR+130; http://en.wikipedia.org/wiki/Return_to_Plain_Awful (1989). Según INDUCKS la única edición en lengua castellana fue en Colombia (1995) con el titulo “Regreso a Cuadrolandia”. Para leerlo online: http://www.zocoi.com/books/142-scrooge-mcduck-return-to-plain-awful
[3] Ice cream soda, http://en.wikipedia.org/wiki/Ice_cream_soda
[4] Freezing-point depression, http://en.wikipedia.org/wiki/Freezing-point_depression
[5] SPANGLER, Steve. The Spangler Effect – Homemade Ice Cream, https://www.youtube.com/watch?v=Y5XzhcDq5Bw
[6] SILVERSTEIN, K. A. T. , HAYMET A. D. J., and DILL, K. A. A Simple Model of Water and the Hydrophobic Effect, J. Am. Chem. Soc. 120, 3166-3175 (1998). doi:10.1021/ja973029k
[7] Bagnoli, Franco. Física de todos los días: los caudales congelados, Revista C2 https://www.revistac2.com/los-caudales-congelados#sthash.YuB7cSdH (2014).
[8] The Fahrenheit scale http://en.wikipedia.org/wiki/Fahrenheit.












