Su notable vida
Antiesclavista. Enemigo de la corrupción. Mártir. Amante de las Matemáticas. De James Abram Garfield la mayor parte de su pueblo solo sabe que fue el vigésimo presidente de Estados Unidos de América. Lo demás ha pasado al olvido.
James Abram Garfield fue el vigésimo presidente de Estados Unidos de América y un apasionado a las matemáticas
Nació en una humilde cabaña de troncos el 19 de noviembre de 1831, en Cuyahoga County. Su padre fue Abram Garfield, emigrado del estado de Nueva York al campo, y Eliza Ballou su madre. A los trece años el joven James era ayudante de carpintero, aunque aprovechaba su tiempo disponible para leer cuanto caía en sus manos. En sus ratos libres resolvía problemas de matemáticas. Cambió su ideal de aventura en la mar por un trabajo en el canal de Ohio que le permitió estudiar y, en 1854, graduarse del Williams College con los máximos honores.
 Fue profesor y director del colegio. En 1859, el Partido Republicano le pidió que fuera candidato para el Senado de Ohio, siendo elegido. Se distinguió inmediatamente por su celo antiesclavista. Estalló la guerra civil y, aunque no tenía experiencia militar, por su prestigio se le encomendó que organizara el 42º Regimiento de Voluntarios de Ohio. Lo hizo tan bien que obtuvo victorias célebres en Kentucky y West Virginia, lo que le confirió el grado de coronel y luego el de brigadier general. La guerra continuó y le dio la oportunidad de ascender a mayor general por su victoria en la famosa batalla de Chickamuaga. Se sabe que Lincoln le dijo una vez: «Ya tengo muchos generales. Usted es más importante en política». Garfield sería elegido nueve veces como congresista. Acariciaba, sin embargo, la idea de retirarse de la política para dedicarse a su carrera de abogado, más pacífica, y a sus lecturas en matemáticas. Pero en 1880 sus partidarios le lanzaron como candidato al Senado de Estados Unidos. Obtuvo una resonante victoria por su gran popularidad, venciendo a su oponente, quien era nada menos que el general Hancock, el vencedor de Gettisburg. El 4 de enero de 1881 fue elegido y juró su cargo de presidente de Estados Unidos. Su determinación se había centrado en combatir la corrupción imperante al interior del Senado y de las instituciones del país, que prácticamente ya era el más poderoso del mundo.
Fue profesor y director del colegio. En 1859, el Partido Republicano le pidió que fuera candidato para el Senado de Ohio, siendo elegido. Se distinguió inmediatamente por su celo antiesclavista. Estalló la guerra civil y, aunque no tenía experiencia militar, por su prestigio se le encomendó que organizara el 42º Regimiento de Voluntarios de Ohio. Lo hizo tan bien que obtuvo victorias célebres en Kentucky y West Virginia, lo que le confirió el grado de coronel y luego el de brigadier general. La guerra continuó y le dio la oportunidad de ascender a mayor general por su victoria en la famosa batalla de Chickamuaga. Se sabe que Lincoln le dijo una vez: «Ya tengo muchos generales. Usted es más importante en política». Garfield sería elegido nueve veces como congresista. Acariciaba, sin embargo, la idea de retirarse de la política para dedicarse a su carrera de abogado, más pacífica, y a sus lecturas en matemáticas. Pero en 1880 sus partidarios le lanzaron como candidato al Senado de Estados Unidos. Obtuvo una resonante victoria por su gran popularidad, venciendo a su oponente, quien era nada menos que el general Hancock, el vencedor de Gettisburg. El 4 de enero de 1881 fue elegido y juró su cargo de presidente de Estados Unidos. Su determinación se había centrado en combatir la corrupción imperante al interior del Senado y de las instituciones del país, que prácticamente ya era el más poderoso del mundo.
Todo enemigo de la corrupción se granjea gratuitamente contrincantes secretos. En su madre patria, mientras él asumía el poder, dos balas calibre 44, una de ellas destinada a alojarse en su cuerpo durante tres meses, se gestaban silenciosamente en una fábrica de armas. Una de las razones por las que se suele recordar a Garfield es la del crimen en su contra seguido de una larga agonía, registrada meticulosamente en los anales de la criminalística norteamericana y de la medicina forense.
El crimen contra Garfield
Apenas cuatro meses después de su toma de posesión como presidente fue asesinado
En la mañana del 2 de julio de 1881, apenas cuatro meses después de su toma de posesión como presidente, Garfield planeaba retirarse unos días a descansar con su esposa a Nueva Jersey. Terminada una reunión urgente y acompañado por el secretario de Estado James G. Blaine y un detective, se dirigió a la estación del viejo ferrocarril de Baltimore y Potomac para tomar el tren. Esa misma mañana, un hombre de cuarenta años, llamado Charles J. Guiteau, de complexión robusta y barba poblada atravesaba caminando Washington hasta la calle 17 cerca del río Potomac. El hombre guardaba en su saco un revólver tipo Bulldog inglés de calibre 44 y se dirigía a una plaza cercana, casi al mismo tiempo que el presidente Garfield se aprestaba a salir de la Casa Blanca. La estación se encontraba cerca de ahí. Eran las 8:30 de la mañana. El hombre alquiló un coche de caballos y le dio la dirección de la estación. Al llegar, pidió al cochero que esperase, se apeó y entró en la estación. A las 9:20 horas el presidente entraba en la estación cogido del brazo de su secretario de Estado. El hombre de la barba cerrada se dirigió hacia ellos. Al ver al presidente, al que reconoció de inmediato, se colocó tranquilamente detrás y a su derecha, y sacando su arma hizo dos disparos sobre él. Al ser detenido exclamó con voz excitada: «Disparé sobre él como una necesidad política, bajo inspiración divina.». Fue la vieja historia repitiéndose nuevamente: el asesino fanático, salido de la nada, con ideas mesiánicas, para matar a un hombre incorruptible. ¿No nos recuerda algo que todos conocemos? Nadie debería dudar que ese crimen fue planeado por enemigos políticos del presidente. Teoría de la conspiración o como quiera llamársele, no debemos olvidar que a causa de estos ardides han caído otros seres notables, como el joven matemático francés Evariste Galois, muerto en un duelo planeado por la policía debido a sus posturas políticas.
Varios médicos fueron llamados urgentemente. Una de las balas había rozado el brazo derecho de Garfield sin producir mayor daño, pero la segunda había penetrado a 3 o 4 pulgadas a la derecha de la columna vertebral, produciendo un orificio de entrada que sangró ligeramente a nivel de la costilla número once, sin salida. Uno de los hombres más valiosos de la historia había caído. En nuestra época esa bala se habría desalojado de inmediato, no habría existido infección, y el héroe se habría salvado. Pero estamos hablado de 1881, año en que aún no había aparatos de rayos X, la cirugía discutía aún los métodos antisépticos y no se conocían ni las sulfamidas, penicilina o antibióticos. Se le introdujeron varias sondas con objeto de determinar el trayecto de la bala sin conseguirlo. El presidente Garfield estaba sentenciado. La opinión de los médicos fue que no viviría mucho y así se lo dijeron. El general aceptó con calma el pronóstico. Lo que siguió fue una angustiosa y prolongada agonía de tres meses en la que Garfield mantenía la conciencia y luchaba por su vida. Finalmente, el 21 de septiembre, murió.
En el cementerio de Lake View, donde está enterrado, puede verse el monumento a su memoria: una torre circular de 50 pies de diámetro y 180 pies de altura, construida sobre una terraza de piedra. La torre contiene relieves que señalan los momentos cruciales de la vida de Garfield. Una estatua del presidente se alza en el interior de la torre. En la estación del ferrocarril de Baltimore-Potomac, aún puede verse una estrella en el suelo señalando el lugar en que el presidente cayó herido.
¡Garfield vive! (Los matemáticos aún lo recuerdan)
Los matemáticos recuerdan al presidente Garfield por otra razón: una demostración original del conocido Teorema de Pitágoras. Si bien no fue un matemático profesional, una de sus mayores pasiones eran las matemáticas, y en tal área dejó una huella imborrable. Como general, esta disciplina le había conferido siempre claridad y rigor de pensamiento.
A muchos generales y militares famosos les ha atraído la Matemática. Uno de ellos fue Napoleón, a quien el genio Laplace, matemático y físico, dedicó su obra. De hecho existe un teorema conocido como el Teorema de Napoleón que muestra qué tan afecto era este estratega a las matemáticas. Brevemente mencionaremos su enunciado sin demostración:
Teorema de Napoleón. Dado un triángulo cualquiera, si se construyen triángulos equiláteros adyacentes a sus lados, los centros de estos conforman los vértices de un triángulo equilátero.
Una ilustración nos muestra lo anterior, para un triángulo ABC:
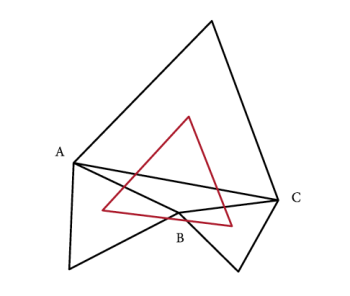
Este es uno de los más hermosos teoremas en geometría, aunque muy posiblemente la demostración se deba al matemático Mascheronni, quien también dedicó su obra matemática a Napoleón y éste, fascinado, la hizo publicar y traducir de inmediato al francés.
Felipe Ángeles, general mexicano y asesor de estrategias militares para la División del Norte, del general Francisco Villa, también era afecto a las matemáticas. Ángeles dejó escritos algunos tratados al respecto, y publicó varios artículos de balística y geometría.
Similarmente, la geometría fue una de las más caras pasiones de James Abram Garfield, a diferencia de otros presidentes norteamericanos: ignorantes supremos de la belleza que existe oculta en el reino matemático, y afectos a la invasión y el exterminio de los débiles. Se ignora si alguna vez alguien animó a Garfield a estudiar matemáticas. Él, siempre fiel a su apego, dedicaba sus momentos de solaz a ellas. Las figuras geométricas le otorgaban una gran paz en momentos de tensión o cansancio. Y el destino le recompensó, fue elegido para que, igual que a unos cuantos, como gustaba decir el matemático húngaro Paul Erdös, Dios le concediese la demostración de uno de los teoremas de su libro transfinito.
Existen cientos de demostraciones del Teorema de Pitágoras que, como es de sobra conocido, reza así (nadie que ame las matemáticas sentirá pesar al repetirlo como un padrenuestro ocasional):
Teorema de Pitágoras. Para todo triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Si la hipotenusa se llama c, y los catetos a y b, la relación de la que hablamos relaciona áreas y se escribe:
a2 + b2 = c2
Se cree que Pitágoras hizo la demostración de este teorema, acaso el más famoso de la Matemática, empleando razonamientos de semejanza de triángulos. La proeza del griego fue que, a diferencia de sus contemporáneos egipcios, babilonios o persas (los chinos conocían mucho antes este hecho y lo habían comprobado para casos particulares), él y sus discípulos lo demostraron no para unos cuantos casos, ni para muchos, sino para todos lo triángulos rectángulos posibles. Eso es lo que hace merecer al teorema el nombre que lleva. Los Elementos de Euclides enuncian otra demostración más compleja que la de Pitágoras, a la que el filósofo Schopenhauer nunca dejó de tildar como una demostración ratonera, pues le resultaba demasiado artificial, aunque sin duda es correcta. La demostración del presidente Garfield, es una de las más conocidas y alabadas por su originalidad.
Observemos el diagrama siguiente:
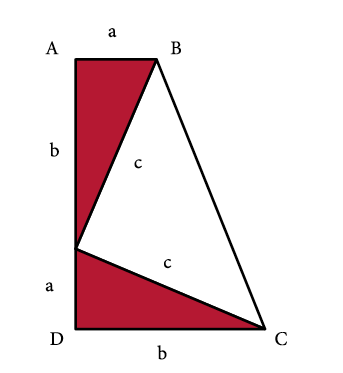 Tal figura trapezoidal está conformada por tres triángulos: dos rectángulos congruentes, de catetos a y b, e hipotenusa c (ambos en rojo), y por uno rectángulo isóceles (en blanco).
Tal figura trapezoidal está conformada por tres triángulos: dos rectángulos congruentes, de catetos a y b, e hipotenusa c (ambos en rojo), y por uno rectángulo isóceles (en blanco).
Garfield razonó así en su demostración:
1 Calculemos el área del trapecio ABCD, con la conocida fórmula para los trapecios:
ÁREA DEL TRAPECIO ABCD =
2 Calculemos esa misma área, la del trapecio ABCD, como la suma de las áreas de los tres triángulos que la conforman: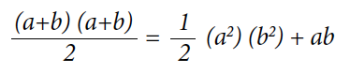
ÁREA DEL TRAPECIO ABCD = 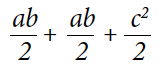
- Igualemos ambos resultados, y simplifiquemos las expresiones algebraicas:
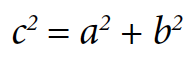 De este modo su demostración del Teorema de Pitágoras estaba concluida.
De este modo su demostración del Teorema de Pitágoras estaba concluida.
¿Por qué se le ocurrió realizarla de tal manera, recurriendo a esa construcción geométrica sui géneris? La respuesta es un misterio. Pero notemos la simplicidad y economía empleada en su razonamiento, producto de sus ratos de divertimento matemático, como solía expresar él.
Especulemos un poco, tan solo con brevedad, y tratemos de entrar a la mente del general. Aventuraremos cómo pudo haber concebido tal prueba. Para ello recordemos uno de los diagramas propuestos por el matemático hindú Bahskara, para ilustrar el teorema, y del cual se desprende una de las demostraciones más conocidas en los textos contemporáneos:
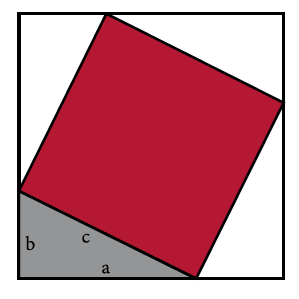 ¿Logra notar el lector algo? De no ser así, disecciónese la figura en dos, de la siguiente manera:
¿Logra notar el lector algo? De no ser así, disecciónese la figura en dos, de la siguiente manera:
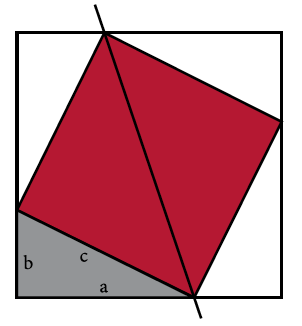 ¡Pues bien!, las dos partes resultantes del dibujo son semejantes al trapecio del que se auxilió Garfield para su célebre demostración.
¡Pues bien!, las dos partes resultantes del dibujo son semejantes al trapecio del que se auxilió Garfield para su célebre demostración.
Quizá podría decirse que la idea de su prueba matemática es muy sencilla. Pero también, y con sobrada justicia, debe responderse que a nadie se la había ocurrido antes. Las cosas simples lo son solo hasta que alguien las ha realizado. Muy pocos han alcanzado la gloria matemática por una demostración tan “simple”. Muchos, sin embargo, han buscado por años esa economía, amiga de la belleza en matemáticas, para demostrar un teorema.
El esbozo de la demostración del presidente de Estados Unidos, James Abram Garfield, límpida y hermosa, debería estar grabada en su tumba, como la que Arquímedes pidió para la suya respecto a su descubrimiento geométrico favorito, o la de Ludoffi, quien calculó con precisión varios dígitos del número π, mucho antes del advenimiento de los computadores. No siempre los dioses conceden tal privilegio, y la piedra debería guardar testimonio de ese atisbo al mundo de lo glorioso y perfecto. C2



carem -
muere el 19 de septiembre
Myriam Laurini -
Me encanta C2 y tu artículo, Isaí Moreno, excelente.