Kepler, canicas y ciencia

Ciencia

Kepler, canicas y ciencia

4 julio, 2017
|
POR Osvaldo Carvente Muñoz
|
0 COMENTARIOS
|
Like 0
|
723

Recuerdo que en mi infancia desbordaba de emoción cuando por las tardes, después de la escuela, comer y hacer la tarea, en la calle del pueblo donde crecí nos reuníamos hermanos, primos y algunos vecinos (casi todos entre 7 y 12 años de edad) para disfrutar el resto de la tarde jugando canicas.

Al terminar el juego, el vencedor alzaba su trofeo: una bolsa con la mayoría de las canicas en su interior. Sin saberlo, me estaba iniciando en el estudio experimental de los medios granulares. En la actualidad me sigo divirtiendo con canicas, pero ahora no se trata de obtener la bolsa con el mayor número, mi juego ahora es en realidad una investigación estrictamente científica.

¿Cómo se comportan las canicas cuando se someten a vibraciones mecánicas?

Mi propósito es desvelar los mecanismos físicos que rigen el comportamiento de esferas más pequeñas que las canicas de mi infancia: entre 1 y 5 milímetros de diámetro, comúnmente conocidas como balines, y que para efectos prácticos siguen siendo canicas. ¿Cómo se comportan cuando se someten a vibraciones mecánicas? Por ejemplo, si hacemos vibrar ligeramente una bolsa llena de balines notaremos que eventualmente van ocupando menos espacio. Desde un punto de vista científico, el sistema evoluciona en forma logarítmica hacia una configuración más densa, conocida como la configuración compacta aleatoria rcp (random close packing por sus siglas en inglés). Sin importar el tiempo que transcurra o la forma de las vibraciones, el resultado siempre es una configuración rcp. En este caso la compactación, definida como la razón del volumen de todas las esferas al volumen del recipiente que ocupan, nunca superará el valor de 0.64.

¿Acaso los balines tienen prohibido auto-organizarse cuando sacudimos la bolsa que los contiene?

Sin embargo, Johannes Kepler, en 1611, afirmó que al apilar esferas idénticas, siguiendo una geometría piramidal, se obtendría la máxima compactación posible (0.74). Dicha afirmación, conocida como la conjetura de Kepler, dio lugar a uno de los problemas más complejos de la geometría discreta. Casi 400 años después, en 1998, Thomas Hales anunció una demostración computacional de la conjetura de Kepler.

¿Acaso los balines tienen prohibido auto-organizarse (cuando sacudimos la bolsa que los contiene) siguiendo la estructura geométrica descrita por Kepler? Hoy sabemos que el apilamiento propuesto por Kepler corresponde a la manera en que, por ejemplo, los átomos de oro se localizan en los vértices y en el centro de las caras de un cubo. Utilizando microscopios de efecto túnel se puede distinguir las posiciones de los átomos individuales sobre alguna superficie metálica como el oro. Reproduciendo espacialmente el cubo, se obtiene una red de átomos, llamada red cristalina centrada en las caras del cubo, o fcc (face centered cubic, por sus siglas en inglés).

A diferencia de los átomos, nuestros balines no son susceptibles a fluctuaciones térmicas…

A diferencia de los átomos, nuestros balines no son susceptibles a fluctuaciones térmicas, así que para inducirlos a explorar el conjunto de estados a los cuales tienen acceso (el espacio fase accesible) se requiere un suministro continuo de energía. Usualmente hacemos vibrar de forma periódica el recipiente que los contiene. Mientras las vibraciones y el número de balines no cambien, se logra compensar la pérdida de energía durante las múltiples colisiones que ocurren y el sistema permanecerá en un estado estacionario. Ahora bien, para tratar de dar respuesta a la pregunta planteada anteriormente, en nuestro grupo de investigación diseñamos un proceso de compactación, que consiste en vibrar sinusoidal y verticalmente un contenedor lleno de balines, pero de tal forma que éstos puedan transitar por diferentes estados estacionarios. Al inicio del proceso se observa una fase semejante a un gas denso y, conforme avanza el tiempo, se pasa por una fase tipo líquida y finaliza en un sólido ordenado. El proceso de compactación, que hemos denominamos recocido vibracional, consiste en ir aumentando en forma sistemática la frecuencia y simultáneamente ir disminuyendo la amplitud de las vibraciones. Así, hemos logramos que un conjunto de balines se auto-organice en el interior de contenedores cuadrados conmensurables. Considerando que los balines ocupan el lugar de los átomos en una red cristalina, la estructura resultante es centrada en el cuerpo del tetrágono (bct body centered tetragonal, por sus siglas en inglés), en la cual la compactación es de 0.69. Aún cuando hemos superado la fase desordenada (rcp), seguimos sin conseguir la configuración que da lugar a la máxima compactación.

Al agregar unas cuantas gotas de aceite a los balines sucede algo inesperado: los balines, ahora con una delgada capa de aceite en su superficie, se auto-organizan durante la vibración en la estructura más densa posible (0.74), la misma que describió Kepler, una fcc [1].

A escala micro-métrica (del orden de 10^-6 m), las partículas coloidales que interactúan únicamente por colisiones, pero susceptibles a un movimiento browniano, muestran una clara tendencia de auto-organización hacia la máxima compactación posible (0.74) conforme aumenta la concentración. En este caso las fluctuaciones térmicas del fluido en el cual están suspendidas las partículas coadyuvan a superar los estados de atascamiento, fenómeno que puede verse en tiempo real con ayuda de un microscopio confocal. A esta escala, ha quedado establecido que el mecanismo físico que promueve la auto-organización es de carácter entrópico. A una escala mucho menor (del orden de 10^-9 m), por ejemplo en películas delgadas para celdas solares, después del crecimiento las películas son sometidas a un proceso de recocido térmico (annealing) que remueve los defectos estructurales, mejorando así la calidad morfológica y logrando celdas más eficientes.

El recocido térmico induce a estados de equilibrio de mínima energía.

Es importante tener en mente que el recocido térmico induce a estados de equilibrio de mínima energía, donde el mínimo queda determinado por un mecanismo de competencia entre la entalpía (debida a las fuerzas de atracción atómicas o intermoleculares) y la entropía. Con respecto a la fenomenología que muestran nuestros sistemas de balines sometidos a vibraciones, podemos decir que presentan propiedades cualitativamente análogas a sistemas susceptibles a perturbaciones térmicas (como las películas delgadas o las partículas brownianas), lo que nos lleva a plantearnos una pregunta fundamental: ¿es posible concebir un marco conceptual, en analogía con sistemas térmicos, que dé sustento físico al proceso de auto-organización de nuestros balines?

Consideremos dos contenedores idénticos llenos de balines, uno en la configuración rcp y el otro en la bct, que se mantienen vibrando de tal manera que no hay reacomodo; las esferas únicamente vibran alrededor de su posición de equilibrio. Si medimos el ruido circundante producido por las múltiples colisiones, resulta que la bct es más ruidosa que la rcp, y midiendo las fluctuaciones de las posiciones de las esferas en un plano vertical (por medio de una cámara de alta velocidad montada perpendicularmente a alguna de las caras del contendor), se puede concluir que el espacio en el que cada esfera puede vibrar es mayor en la bct, y que la configuración rcp está en un estado de bloqueo (jamming). Por tanto, el mecanismo físico que da lugar a la estructura bct de balines es, en analogía con partículas coloidales, el aumento de entropía. Por otra parte, la capa de aceite crea puentes de líquido entre las esferas que están suficientemente cerca unas de otras, y el resultado global es una fuerza capilar de cohesión tipo van der Waals.

Entonces, en analogía con sistemas térmicos, la fuerza capilar de atracción da como resultado una energía de cohesión que es equivalente a la entalpía, y por tanto el mecanismo físico que da la lugar a la auto-organización fcc es una competencia entre la energía cohesiva y la energía de vibración de los balines. Esta última directamente relacionada con la entropía según la concepción de Boltzman [2]. El marco conceptual descrito, de ser correcto, debe ser predictivo y poder aplicarse exitosamente a otros tipos de fuerzas de atracción. Por ejemplo, si ahora la fuerza de atracción se debe a una magnetización remanente de los balines, después de ser retirados de las cercanías de un campo magnético (un imán) y sometidos al recocido vibracional, el resultado es la auto-organización de los balines magnetizados en la estructura fcc [3]. Por otra parte, si aumentamos la magnitud de las vibraciones durante el proceso de recocido el efecto de la fuerza cohesiva (capilar o magnética) se reduce a prácticamente cero, los balines se comportarán como esferas duras, y nuestro marco conceptual predice en este caso una auto-organización tipo bct. Al realizar el experimento hemos corroborado dicha predicción.

Debido al carácter disipativo de la fuerza de fricción, y a las múltiples colisiones inelásticas, es prácticamente imposible resolver analíticamente las ecuaciones de Newton y predecir la dinámica de los medios granulares. Sin embargo, por medio de simulaciones de dinámica molecular hemos podido corroborar los resultados experimentales arriba descritos, es decir, en contenedores conmensurables sometidos al recocido vibracional. La estructura bct se obtiene con esferas no cohesivas, mientras que la fcc únicamente se obtiene con esferas cohesivas.

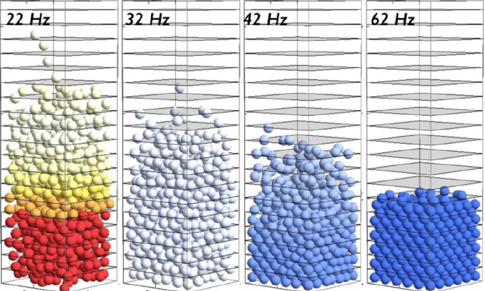
Con respecto a la experimentación, las simulaciones numéricas proporcionan un mayor alcance científico, ya que ahora podemos cuantificar, por ejemplo, la compactación local, la temperatura granular y el número de coordinación para cada uno de los estados estacionarios por los que transitan los balines durante en recocido vibracional, desde la fase gaseosa hasta la sólida. Nuestros últimos resultados (computacionales) han mostrado que durante el proceso de auto-organización aparecen pequeñas regiones donde el factor de empaquetamiento es constante (llamadas puntos isodensos), y que el gradiente de temperatura granular sufre un cambio de dirección (justo antes del cambio de dirección la temperatura granular es constante, punto isotérmico). Interesantemente, alrededor del punto isotérmico comienza una transición estructural de fase de primer orden, cuantificada por la aparición de regiones de balines con el número de coordinación máximo (10 y 12 para la bct y fcc, respectivamente). Finalmente, de los resultados computacionales se estableció una relación analítica entre los valores de la compactación y la temperatura granular a nivel local para todos los procesos de auto-organización estudiados [4] .

No cabe duda que la ciencia puede estar frente a nuestros ojos, sólo es cuestión de ponerle un ojo científico a nuestros juegos. C²

Referencias

[1] Phys. Rev. Lett. 95, 018001 (2005).

[2] Phys. Rev. E, 78, 011302 (2008).

[3] Granular Matter 14, 303-308 (2012).

[4] Phys. Rev. E 93, 020902(R), (2016).

Sobre el autor

Osvaldo Carvente Muñoz

Facultad de Ingeniería, UADY

Profesor Investigador Titular C de tiempo completo en la Facultad de Ingeniería de la Universidad Autónoma de Yucatán y miembro del Sistema Nacional de Investigadores, Nivel I. Su principal línea de investigación es el estudio de la dinámica de medios granulares bajo perturbaciones externas, llevada a cabo mediante experimentos y simulaciones de dinámica molecular.