El problema de Dido es un clásico de las matemáticas, e incluso de la literatura y de la historia.
De acuerdo con Virgilio [1], Dido se suicida después de haber sido abandonada por Eneas y a este hecho se remonta la oposición entre los romanos y los cartagineses.
Dido ordenó que se cortara la piel en tiras finas, que luego serían juntadas en los extremos para formar una cuerda larga.
Otra versión es que la princesa Dido huye con algunos fieles, de su ciudad natal de Tiro, después de descubrir que el rey Pigmalión (su hermano, nada que ver con el escultor griego del mismo nombre) había matado a su marido. Después de un largo viaje aterriza en la costa norte de África (Libia). Allí se encuentra con el rey Jarbas para comprar una parcela de terreno sobre la cual construir una nueva ciudad. El rey, en respuesta, le responde que puede tomar cuanta tierra pudiera encerrar la piel de un toro. Virgilio no describe cómo Dido resolvió el problema. Sin embargo, la tradición dice que la princesa, sin perder el corazón, ideó una estratagema para tomar la tierra más vasta posible. Dido ordenó que se cortara la piel en tiras finas, que luego serían juntadas en los extremos para formar una cuerda larga.
Con esta cuerda, la princesa rodeó una colina (sobre la cual deseaba construir la fortaleza), colocando los extremos de la cuerda en el mar. También dice que Dido tuvo que arreglar la cuerda en la forma de un semicírculo de manera de encerrar la mayor superficie posible.
El problema de Dido en matemáticas se resume a cómo encontrar la figura que tiene la mayor área de superficie dada su perímetro.
El problema de Dido en matemáticas se resume a cómo encontrar la figura que tiene la mayor área de superficie dada su perímetro. En un plano la solución es un círculo; en un semiplano, un semicírculo.
Aunque el problema puede parecer trivial, su solución requiere un conocimiento de cálculo de variaciones [2] dada la complejidad técnica del problema.
Si dibujamos una curva cerrada en una esfera, no está claro qué es lo “interior” y lo “exterior”.
Ahora vamos a examinar el problema a través de los ojos de un físico. En primer lugar, podemos decir que la mejor manera de agarrar la tierra con un perímetro determinado (la cuerda hecha de la piel), sin contar las costas, es encontrar una península separada por un istmo de ancho igual a la cuerda disponible. Así que no hay límite a la tierra obtenible. Por otra parte, no vivimos en un plano sino en la Tierra, que es similar a una esfera. Si dibujamos una curva cerrada en una esfera, no está claro qué es lo “interior” y lo “exterior”. Dido pudiera haber pedido toda la Tierra excepto la pieza rodeada por su cuerda! Pero es probable que el rey Jarbas no hubiera estado de acuerdo.
El otro elemento muy importante en el que nadie se detiene es: ¿cuán larga puede ser una cuerda hecha de la piel de un toro?
Hace tres mil años la tecnología, desde luego, no era capaz de convertir de este modo una piel de toro.
Al aplicar las leyes de la física, la cuerda más larga (dada una cierta masa) se puede hacer con una cadena polimérica, un tipo de hidrocarburo, una cadena de ADN o un microtúbulo proteico o de carbono. Pero hace tres mil años la tecnología, desde luego, no era capaz de convertir de este modo una piel de toro, por no mencionar que estos filamentos son invisibles y extremadamente frágiles.
Supongamos entonces que hay que cortar la piel sin hacer transformaciones físicas o químicas. Para simplificar, digamos que la piel cubre 1 metro cuadrado (probablemente será tres o cuatro, pero sólo cambia un factor), que es perfectamente bidimensional (aunque en su lugar tiene un cierto espesor) y que se puede cortar al máximo en filamentos gruesos de 1 milímetro (empresa no trivial). Se obtienen así 1,000 metros de cuerda, que, sin embargo, aún debe ser anudada (con 1000 nudos).
Usando nudos planos simples [3], he estimado que cada nudo “consume” un pedazo de hilo de largo de más o menos 10 veces su diámetro. Por lo que se pierden en total 10 metros de cable, que no es mucho. ¿Podemos ahorrarnos los nudos? Sí, escogiendo cómo cortar la piel del búfalo. Para demostrar esto de una manera práctica, desafiamos a un amigo a pasar a través de una puerta dibujada en una pequeña hoja de papel.
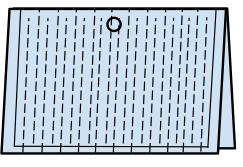
Dibujamos en un cuarto de una hoja A4 una puerta doble. Doblamos el papel por la mitad y cortamos a lo largo de las líneas de puntos (no cortar completamente a lo largo del pliegue, se debe dejar las dos extremidades intactas)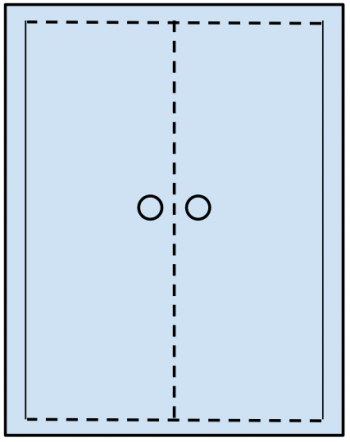
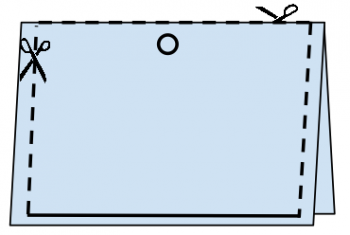
Desdoblando la hoja, la puerta ahora se puede abrir, pero será imposible pasar.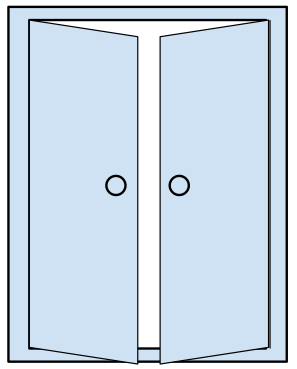
En este punto tenemos que doblar la hoja de nuevo y hacer más cortes de acuerdo con las nuevas líneas de puntos en la figura (la lineas parten de forma alternativa de la flexión y desde el borde).
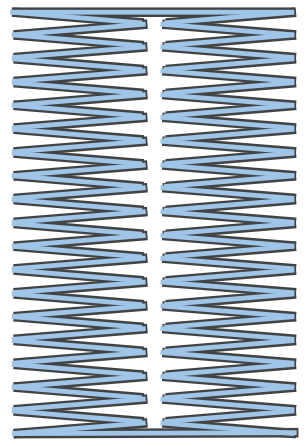
Esta vez la puerta se abrirá en forma de zig-zag y puede expandirse lo suficiente para pasar a través de ella. C2
Referencias
[1] Eneida, Libro I, verso 365-369
[2] https://mathematicalgarden.wordpress.com/2008/12/21/the-problem-of-dido/
[3] https://en.wikipedia.org/wiki/Reef_knot
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
- Franco Bagnolihttps://www.revistac2.com/autor/franco-bagnoli/
