La sustancia simbólica
Los objetos del mundo material tienen densidad, volumen, temperatura o algunas otras propiedades. Sin embargo, el mundo humano no está hecho solamente de objetos materiales. Existe la amistad, la educación, la Suprema Corte de Justicia. Y ninguna de estas “cosas” tienen peso, volumen o temperatura. Están hechas de otra sustancia.
A lo largo de nuestra estancia en el planeta, los seres humanos fuimos adquiriendo diversas habilidades que gradualmente nos acercaron a lo que somos hoy, desarrollando la sociedad mano/herramienta, que permitió la producción de innumerables artefactos orientados a la supervivencia de la especie.
Un punto de inflexión en el desarrollo de nuestros ancestros tuvo lugar en el momento en que adquirimos capacidad simbólica.
Un punto de inflexión en el desarrollo de nuestros ancestros tuvo lugar en el momento en que adquirimos capacidad simbólica. Cuando algún antepasado hizo una serie de incisiones sobre un hueso para significar piezas de caza, reveló que estaba en posesión de esta capacidad. Una incisión no es un conejo pero toma el lugar del (posible) conejo. Un símbolo, lo sabemos, es cualquier cosa que toma el lugar de otra que (posiblemente) se encuentra ausente. El significado de un símbolo suele resultar de una convención, de un acuerdo entre los miembros de un grupo — que puede ser tan grande como los hablantes de una lengua. Entonces, cuando uno de nuestros ancestros está ante una tibia de lobo con incisiones, entiende que, en su grupo, eso significa el resultado de la caza del día anterior.
La capacidad simbólica tiene una larga y fascinante historia, pero tal vez la más fascinante es la que tiene que ver con la adquisición del lenguaje. El cuerpo mismo ha sido nuestro espacio de representación primigenio. Gestos faciales, miradas, sonidos guturales y finalmente la lengua en todo su esplendor. Sus orígenes se pierden en el tiempo pero no así las huellas que fueron dejando los sucesivos niveles de comunicación tanto en la organización social como en la producción material de herramientas para la supervivencia, cada vez más sofisticadas.
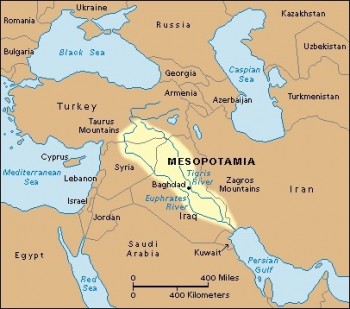 Hace unos cinco mil años, en Mesopotamia, los sumerios iniciaron lo que iba a convertirse en una verdadera revolución cognitiva. Mesopotamia quiere decir entre ríos. El Tigris y el Eufrates, y la abundancia de barro hizo viable que la superficie de su escritura (la primera de la que se tiene registro) fuese, justamente, una tablilla de barro. Una tablilla con hendiduras hechas en forma de cuña y de allí su nombre: escritura cuneiforme. La historia de esta invención ha sido narrada con lujo de detalles por Denise Schmandt-Besserat en su extraordinario libro How Writing Came About (UTexas, Austin). Allí se narra cómo la invención de la escritura llegó de la mano de otra invención: un sistema numérico posicional (sexagesimal), cuyo impacto sigue vigente en medio de los cotidianos grados, minutos y segundos.
Hace unos cinco mil años, en Mesopotamia, los sumerios iniciaron lo que iba a convertirse en una verdadera revolución cognitiva. Mesopotamia quiere decir entre ríos. El Tigris y el Eufrates, y la abundancia de barro hizo viable que la superficie de su escritura (la primera de la que se tiene registro) fuese, justamente, una tablilla de barro. Una tablilla con hendiduras hechas en forma de cuña y de allí su nombre: escritura cuneiforme. La historia de esta invención ha sido narrada con lujo de detalles por Denise Schmandt-Besserat en su extraordinario libro How Writing Came About (UTexas, Austin). Allí se narra cómo la invención de la escritura llegó de la mano de otra invención: un sistema numérico posicional (sexagesimal), cuyo impacto sigue vigente en medio de los cotidianos grados, minutos y segundos.
El impacto que ha tenido la escritura desde entonces ha sido enorme. Primero, suministró un soporte externo para la memoria y muy pronto se constituyó en un espacio cognitivo. Cada vez que leemos un escrito
 propio, por ejemplo, reorganizamos nuestras ideas y las vamos puliendo en un proceso que recuerda al trabajo de un escultor. Ya en la Grecia clásica Platón en uno de sus diálogos, Fedro, que tiene como figura protagónica a Sócrates, le hace decir a éste que la escritura destruye la memoria y debilita la mente al liberarla del trabajo que la hace fuerte. La irrupción de la escritura en el universo griego transformó de raíz su cultura. Estamos escribiendo sobre algo que tuvo lugar hace más de 25 siglos y que fue una de las causas de lo que se ha llamado el Milagro Griego y que ha sido entendido como la raíz del pensamiento científico occidental. Hay un dejo irónico en todo esto: tal vez no tendríamos noticias sobre Platón hoy en día si él no hubiese cedido a la tentación de escribir. La escritura es la máquina del tiempo que lo trae hasta nosotros.
propio, por ejemplo, reorganizamos nuestras ideas y las vamos puliendo en un proceso que recuerda al trabajo de un escultor. Ya en la Grecia clásica Platón en uno de sus diálogos, Fedro, que tiene como figura protagónica a Sócrates, le hace decir a éste que la escritura destruye la memoria y debilita la mente al liberarla del trabajo que la hace fuerte. La irrupción de la escritura en el universo griego transformó de raíz su cultura. Estamos escribiendo sobre algo que tuvo lugar hace más de 25 siglos y que fue una de las causas de lo que se ha llamado el Milagro Griego y que ha sido entendido como la raíz del pensamiento científico occidental. Hay un dejo irónico en todo esto: tal vez no tendríamos noticias sobre Platón hoy en día si él no hubiese cedido a la tentación de escribir. La escritura es la máquina del tiempo que lo trae hasta nosotros.
No cabe duda que la escritura puede ser considerada la corona de todo ese esfuerzo milenario que empezó con un gesto que hendió un filo sobre un hueso y que nos trajo hasta las orillas del alfabeto y del sistema decimal.
Si mañana leyésemos en el periódico que los números naturales han desaparecido, no tendríamos duda alguna que se trata de una broma. Tenemos certeza que se trata de algo imposible. O casi. ¿De dónde proviene esa certeza sobre la existencia tan estable de los números naturales? No tienen peso ni densidad. No tienen color ni temperatura pero ahí están, levantando la mano durante todo el día. Sin ellos no hay horas ni cumpleaños —aunque haya tiempo. Entonces ¿de qué sustancia están hechos que se hacen notar de maneras tan conspicuas? Igual que el alfabeto, están hechos de una sustancia simbólica. Uno puede pensar que es inevitable ver la numerosidad en lo que nos rodea y así es. Más aún, se puede pensar que algunas otras especies tienen también un sentido de la numerosidad. Pero una cosa es esa expresión rudimentaria de la numerosidad y otra muy distinta el número como cristalización simbólica de la acción humana de contar. Nuestro ancestro que marcaba huesos para llevar sus cuentas transitaba, digámoslo así, de la numerosidad al número. Sin embargo, estaba demasiado anclado a su contexto para que aquellas marcas pudiesen interpretarse como el seis de hoy: seis manzanas, seis investigadores, seis de lo que usted quiera. El número ha dejado atrás todos los contextos. Tiene un alto grado de abstracción —entendida como el resultado del esfuerzo por extraer la estructura.
“Todo aquello que dibujamos y escribimos sobre una superficie son las sombras de los verdaderos objetos”
Platón explicaba que todo aquello que dibujamos y escribimos sobre una superficie son las sombras de los verdaderos objetos que existen en toda su plenitud en un lugar que él denominó el Topos Uranus. Ese era el mundo donde existían los números, los triángulos y demás objetos reconocidos por la cultura matemática griega. Aquellos símbolos y grafías pues, no eran sino las sombras de los verdaderos seres, de los que existían realmente pero en la realidad del Topos Uranus. Esa sensación de realidad que se percibe y que otorga tanta confianza cuando uno está enfrascado en la resolución de un problema, ha hecho que una gran parte de los matemáticos profesionales de diversas épocas se hayan confesado platónicos.
La apropiación del conocimiento
Ir mas allá de los números para contar puede generar en muchos aprendices la sensación de estar entrando en un territorio lejano, puramente simbólico. Un día llega el profesor y anuncia: entre los números impares: 3, 5, 7, 9, 11, 13, 15, etc., hay algunos que pueden expresarse como un producto. Por ejemplo, 9 puede expresarse como 3×3, 15 como 3×5, pero 17 no. Este 17 está hecho de un solo bloque. También el 3 está hecho de un solo bloque. Aquí empieza una exploración que puede generar un sentimiento de fascinación a estudiantes muy jóvenes: tratar de hacer la lista de aquellos que son un solo bloque. Por ejemplo, 3,5, 7, no se pueden escribir como un producto (queda excluida la multiplicación por 1). Una calculadora de las más sencillas puede tornarse un socio muy importante en la elaboración de la lista. Los estudiantes pueden diseñar estrategias para encontrar números menores que 100, digamos, que no puedan escribirse como producto. El problema adquiere gradualmente mayor complejidad si empezamos a explorar más allá del 100. Esta clase de preguntas ya están muy lejos de los conejos que nuestros ancestros representaban como incisiones sobre un hueso. El estudiante inicia ahora un viaje guiado tan solo por reglas operatorias formales. Mientras permanezcamos “cerca” de los números naturales, no hay un riesgo grande de que los estudiantes se extravíen y puedan avanzar poco a poco en el proceso de apropiación del sistema numérico. Es una experiencia que el estudiante adquiere en un territorio culturalmente codificado mediante símbolos matemáticos. Basta entonces recorrer someramente la historia de las matemáticas para corroborar que el progreso siempre estuvo de la mano de algún sistema de representación simbólico que suministraba la posibilidad de hacer operaciones. Debo enfatizar que la representación simbólica de una idea matemática no es una vestimenta casual para esa idea sino que ésta es inseparable de la representación. Así como el sonido y la música.
Aprendizaje: territorio en donde se funde lo subjetivo con lo objetivo.
He vivido las matemáticas casi todo el tiempo desde el salón de clases y acompañando las reflexiones de colegas tan perplejos como yo mismo ante las condiciones casi invisibles del aprendizaje. El aprendizaje de seres que tienen el mismo nivel de complejidad que el observador. Aprendizaje: territorio en donde se funde lo subjetivo con lo objetivo. Se funden, porque aprender es volver a vivir el conocimiento. Desafortunadamente no siempre se tiene conciencia de ello. Hace unos años tuve un profesor que hablaba lentamente y de manera reflexiva pero siempre dirigiéndose a sí mismo. En medio de una explicación se detenía como obedeciendo una orden interna mientras sostenía un diálogo privado sobre algo que le inquietaba, que venía a su mente en aquel momento. Para él era como un instante de sosiego mientras, con aire un poco distraído, estiraba el brazo mientras su índice recorría una curva muy suave tratando de hallar, de sentir un punto de inflexión en aquella gráfica que él percibía en un espacio imaginario. No dudo que sea casi imposible vivir las matemáticas al margen de esa realidad tangible de un mundo poblado de seres invisibles pero que distan mucho de ser evanescentes. Tal vez habría empleado otras palabras pero, estoy seguro, que aquel profesor creía que esos seres vivían en un mundo inmaterial pero tan real como las piedras. Nosotros, sus alumnos, veíamos aquella escena con mucha curiosidad. Nos preguntábamos entonces en qué estaría pensando cuando caía en aquellos trances tan placenteros a simple vista pero desconocidos para los demás. Algunos perseveramos, tal vez asistidos por un fuerte sentimiento de curiosidad, pero casi todos renunciaron a tratar de penetrar en aquella realidad escondida.
¿Acaso la educación tiene que ser un proceso cruelmente darwiniano?
Creo que ninguno de nosotros estaría dispuesto a dar una respuesta positiva a esta interrogante. Pero es claro que responder involucra mucho más que un catálogo de buenas intenciones. Aún hoy en día se suele escuchar que para enseñar “bien” las matemáticas hay que saber matemáticas. Una respuesta digna de Perogrullo. En efecto, hay que saber matemáticas, pero ¿cómo debe ser ese saber?
No pretendo dar respuesta, en estas líneas, a una pregunta tan compleja que ha requerido mucha investigación intra, inter y trans disciplinar. Sin embargo, hay ideas que el campo de la didáctica de las matemáticas ha puesto sobre mi mesa. Una de ellas afirma que disolver las dificultades que enfrentan los alumnos pasa por investigar el modo de existencia y el desarrollo del significado de los entes/objetos matemáticos. Es menester estudiar este problema desde la perspectiva del investigador mucho antes de someterlo a la ingeniería del diseño curricular. En efecto, no se logra hacer tangible, palpable la realidad de los entes matemáticos si se les aísla del terreno de la experiencia de los estudiantes. Y eso lo muestra la investigación de campo. La experiencia numérica, digamos, se va desarrollando gradualmente y llega un momento cuando se hace viable el pasaje a la exploración interna del sistema numérico, es decir, la exploración de las reglas con las que se operan los propios símbolos.
Las matemáticas son tal vez la forma más simple de conocimiento científico.
Las matemáticas son tal vez la forma más simple de conocimiento científico. Simple no quiere decir trivial en el sentido justamente que los matemáticos atribuyen al vocablo de marras. Los sumerios vivieron el ruido de lo concreto-cotidiano hasta el momento en que lograron descontextualizar sus sistemas numéricos. Lo abstracto es simple y a la vez polisémico y de allí la enorme riqueza interpretativa de los hechos matemáticos. Una ecuación por ejemplo, sirve para modelar innumerables situaciones físicas, como la ecuación de onda que describe la luz y también el sonido entre otros fenómenos de carácter ondulatorio.
La intuición y el análisis
Todo lo anterior me lleva a una reflexión final sobre los mecanismos de conocer y su dimensión simbólica. Los seres humanos poseemos una forma de conocer híbrida y por lo tanto nuestro conocimiento también es híbrido. El lunes mientras leemos un artículo intuimos que la afirmación del autor puede no ser válida. No sabríamos en ese momento argumentar lógicamente sobre el porqué de nuestra aseveración pero sentimos que tenemos razón. Más tarde, después de un esfuerzo sostenido, logramos dar con una argumentación que no deja duda alguna: teníamos razón. Es decir, nuestra intuición era correcta. Es como si tuviésemos un mecanismo cognitivo que se adelanta al razonamiento lógico. Desde luego no siempre es así pero a medida que profundizamos en un campo, esas intuiciones se van haciendo más certeras— al tiempo que nuestra prudencia intelectual aumenta. Este conflicto que parece emerger entre dos formas de conocer (la intuición y lo analítico) también tiene una identidad que ha sido investigada desde las neurociencias. Merlin Donald ( A Mind so Rare, 2001) sostiene que a lo largo del desarrollo filogenético, el universo trabajó como un escultor sobre el sistema nervioso fijando en él su propia imagen y, en consecuencia, generando respuestas viables de una especie frente a su entorno. Esa forma de inteligencia instalada en el sistema nervioso, que nosotros también habríamos heredado, nos permitiría un trato directo con el entorno —ahora saturado por la acción humana—revelando las aristas de eso que llamamos pensamiento intuitivo. Si es cierto que nuestra capacidad predictiva tiene su origen y necesidad en el movimiento (I of the Vortex, R. Llinás, 2001, MIT), eso explicaría la sensibilidad ante todo lo que se mueve. Una mariposa en estado de absoluta quietud es invisible sobre la corteza del árbol, pero revela su presencia a través del movimiento. En los seres humanos, el control consciente de los movimientos del cuerpo nos regaló una mano tan fina y flexible que Kant la llamó la parte visible del cerebro. La mano nos regaló, además, la posibilidad del lenguaje articulado (The Hand and the Brain, G. Lundborg, 2014, Springer). Han sido tan profundas las consecuencias de esta conciencia del movimiento, que gran parte de los esfuerzos matemáticos desde hace ya siglos, han consistido en re-describir el movimiento en términos simbólicos. Uno de los resultados más profundos ha consistido en el desarrollo de las matemáticas de la variación y la acumulación cuya versión clásica, el cálculo infinitesimal se tornó uno de los recursos predictivos centrales de las ciencias físicas. Hoy en día, la tecnología contemporánea ha permitido la simulación del movimiento sobre las pantallas digitales y con ello la educación adquiere un instrumento de mediación que puede detonar una nueva convergencia entre el pensamiento corporizado y el pensamiento simbólico, pero ahora en el escenario de la cultura humana. C2