Antes de su prematura muerte en 1949, el lingüista George Kingsley Zipf decidió estudiar mediante una técnica insólita la novela Ulises de James Joyce. Zipf se aventuró en realizar un análisis estadístico de las palabras utilizadas por Joyce, contando cuántas veces se repetía cada palabra en el texto. Luego las ordenó en una lista, poniendo la palabra más usada al principio, la siguiente más usada en segundo lugar, y así sucesivamente. La palabra más rara quedaba al final de la lista. Al orden de una palabra en esta lista le llamó “rango” (a este proceso de ordenamiento se le llama en inglés ranking). Podemos pensar en este ordenamiento por número de apariciones como una jerarquización, una “lista de popularidad” de palabras en un texto.
Consideremos por ejemplo un texto típico en español. El principio de la lista ordenada luce así:
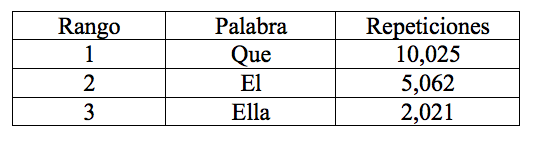
Este método se ha vuelto muy popular en otros campos para dar criterios de valoración. Por ejemplo, para designar a las 100 personas más ricas, a los 10 mejores jugadores de tenis, los 10 artistas más influyentes, los 100 mejores discos , las 10 mejores compañías donde trabajar, etc., usando en cada caso criterios de frecuencia como cantidad de dinero ganada, partidos ganados, discos vendidos, etc. Hay páginas de internet dedicadas a esta tarea de clasificar, por ejemplo: http://fortune.com/rankings.
Zipf encontró que existía una relación matemática entre el rango y el número de veces que aparece una palabra en un texto dado. Así, de modo aproximado, la palabra más usada aparece en un texto el doble de veces que la segunda, la tercera el triple, la cuarta el cuádruple y así sucesivamente. Esta ley puede resumirse así: el rango (r) y el número de repeticiones, usualmente llamado frecuencia (f), son casi inversos uno de otro. A este hecho empírico se le llama Ley de Zipf.
En realidad, esta ley se puede hacer de manera un poco más exacta mediante un ajuste matemático de los datos para un texto u autor dado. La famosa fórmula empírica de Zipf es la siguiente:
f = constante/ra
donde el exponente a es un número muy parecido a uno. Después de Zipf, esta ley se ha verificado para numerosos lenguajes, incluyendo el náhuatl. También es válida para lenguajes de computación, así como para el lenguaje universal de programación de la naturaleza: el ADN. El exponente a depende ligeramente del autor y de la lengua.
El exponente a vale casi siempre uno, con pequeñas diferencias dependiendo del autor, la época, etc. Por ello es común oír decir que la ley de Zipf indica que la frecuencia de las palabras decrece como su rango. Así, la palabra con rango 2 aparece ½ de veces respecto a la de rango 1, mientras que la de rango 3 aparece 1/3 de veces, la de rango 4 está ¼ de veces, etc.
A modo de ejemplo podemos citar que, normalmente para un buen autor, las diez palabras más frecuentes aparecen cerca de un 25% de las veces. En textos de autores con un vocabulario más pobre, este porcentaje sube hasta un 30%. La diferencia no es mucha, lo cual muestra que el buen escritor no puede evitar utilizar las palabras más frecuentes, como artículos, preposiciones, etc. Éstas las utiliza prácticamente tanto como el mal escritor. Curiosamente, los textos con mayor uso de vocabulario corresponden a textos legales.
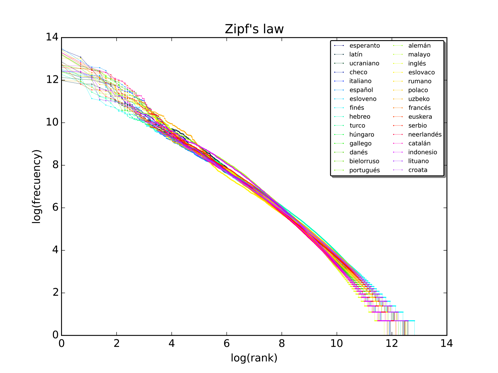
Una manera muy común de confirmar la ley de Zipf es graficar la frecuencia contra el rango. Más aún, dado que la ley de Zipf implica una ley de potencias, normalmente se prefiere graficar usando una función matemática conocida como logaritmo, la cual hace aparecer las leyes de potencias como si fueran rectas. Así, en la Figura 1 presentamos dicha gráfica para el rango-frecuencia de muy diversos idiomas, usando para ello la función logaritmo. Puede verse claramente que todas las curvas son muy parecidas y se ajustan bastante bien a una recta (excepto en los extremos, lo cual se discutirá después).
Desde luego, a partir del trabajo de Zipf se ha empezado a trabajar con combinaciones de palabras e incluso ideogramas para el caso del chino. También con la frecuencia de distancias entre palabras así como la época en que fueron escritos los textos.
En realidad se sabe que la ley de Zipf deja de funcionar exactamente para las palabras más raras y las más frecuentes. Esto se debe a que Zipf consideró sólo unas pocas palabras, pero si se hace esto con una computadora y bases de datos grandes, se observan otros efectos. Una ley que ha sido muy bien acogida dado que sólo modifica ligeramente la ley de Zipf es la llamada ley beta modificada, desarrollada en el Instituto de Física de la UNAM. Esta ley contiene a la de Zipf y reproduce mejor que otras todo el espectro de rangos [Naumis2008]. Dicha ley tiene la forma,
f = C(N+1-r)b/ra
donde N es el rango de la palabra más rara, y tanto a como b se ajustan de los datos obtenidos para un lenguaje dado. C es un número constante para un texto dado [Naumis2008]. Su calidad en el ajuste y sencillez han mejorado la ley de Zipf, lo cual se ha confirmado en numerosos lenguajes tales como en el chino escrito y hablado [Li2013].
Zipf trató de explicar esta ley con el principio de mínimo esfuerzo, haciendo notar que los monosílabos son más comunes que las palabras con muchas sílabas, postulando de este modo una especie de teoría de evolución del lenguaje. Sin embargo, es aquí donde la historia se vuelve complicada. Resulta que la ley de Zipf en realidad ya había sido observada en campos de la ciencia tan diversos como rangos de sismos (ley de Herr), crecimiento de ciudades (ley de Yule-Simon), riqueza (ley de Parteo) y en especial para sistemas con propiedades fractales. Nos referimos aquí a los llamados sistemas complejos, en los cuales existen muchas unidades interactuantes entre sí que dan lugar a comportamientos emergentes. Piense el lector en el caso del tráfico, donde los conductores de manera individual dan lugar a un comportamiento colectivo muy cercano al de los líquidos o sólidos (cuando hay congestionamientos). Estos “ruidos” se comportan como 1/f, y aparecen en circuitos electrónicos, avalanchas, crecidas de ríos, errores de transmisión en líneas de comunicación, en el corazón, etc. Para complicar la historia, la música sigue la ley de Zipf.
![Tabla 1. Parámetros a y b de la ley beta-modificada [Naumis2008] para diversos lenguajes, obras musicales y secuencias genéticas.](https://www.revistac2.com/c2/wp-content/uploads/2017/02/2.png?x15962)
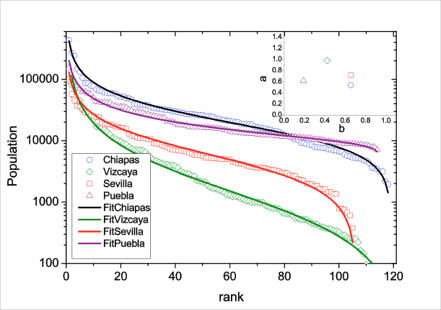
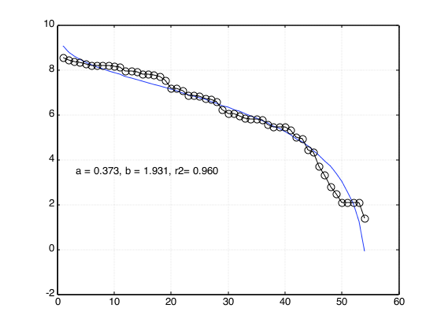
Desde luego, la ley beta modificada también reproduce bien los casos anteriores, incluyendo el ADN de diversos organismos, avalanchas, terremotos, etc. En la Tabla 1 presentamos un resumen comparativo entre lenguajes, música y secuencias genéticas. Como puede verse, los valores son bastante parecidos. Para apreciar visualmente este hecho, en las Figuras 2 y 3 presentamos dos ejemplos en campos muy diferentes: una población en diversas localidades y las notas en la música de Bach. De hecho, su uso ha sido extendida a la popularidad de los nombres de niños en China, crecidas del río Arno en Italia, crecimiento de ciudades en Israel. Recientemente, sus parámetros se han propuesto como una manera de representar el rango de los científicos, de modo que se sustituya por el factor h de Hirsh [Petersen2012].
La pregunta aquí es si estas son coincidencias debido a cuestiones dictadas por el azar (o por el azar con cierta dosis de predictibilidad) o si existe la posibilidad de algo mucho más profundo en todo esto.
Por ejemplo, George Miller y posteriormente Wentan Li consideraron hace algunos años la estadística de un ejército de monos escribiendo al azar, tal y como se nos cuenta en el cuento La biblioteca de Babel de Jorge Luis Borges. El resultado fue algo bastante parecido a la ley de Zipf. Usando otros mecanismos tales como azar controlado, se obtienen leyes más parecidas a la de Zipf. El problema con todo esto es que en realidad, como queda claro en el cuento de Borges, las construcciones habladas no se emiten de forma aleatoria. El enigma aquí es tratar de decidir entre los diversos modelos existentes o formular otros basados en los datos empíricos. Sorprendentemente, no existen a la fecha evidencias conclusivas a favor o en contra de los diversos modelos. Tal vez porque hay más gente interesada en formular modelos que en buscar caminos para validarlos, o tal vez simplemente hay algo que se nos escapa. Tampoco existe claridad en si las coincidencias con otros campos son hechos estadísticos universales (como la llamada distribución normal o Gaussiana) o si sólo son superficialmente parecidos.
En pocas palabras, podríamos empezar a sentirnos como en el famoso cuento de Borges:
La Biblioteca incluye todas las estructuras verbales, todas las variaciones que permiten los veinticinco símbolos ortográficos, pero no un sólo disparate absoluto. Inútil observar que el mejor volumen de los muchos hexágonos que administro se titula «Trueno peinado», y otro «El calambre de yeso» y otro «Axaxaxas mlo». Esas proposiciones, a primera vista incoherentes, sin duda son capaces de una justificación criptográfica o alegórica; esa justificación es verbal y, ex hypothesi, ya figura en la Biblioteca. No puedo combinar unos caracteres dhcmrlchtdj que la divina Biblioteca no haya previsto y que en alguna de sus lenguas secretas no encierren un terrible sentido. Nadie puede articular una sílaba que no esté llena de ternuras y de temores; que no sea en alguno de esos lenguajes el nombre poderoso de un dios. Hablar es incurrir en tautologías. Esta epístola inútil y palabrera ya existe en uno de los treinta volúmenes de los cinco anaqueles de uno de los incontables hexágonos, y también su refutación. (Un número n de lenguajes posibles usa el mismo vocabulario; en algunos, el símbolo biblioteca admite la correcta definición ubicuo y perdurable sistema de galerías hexagonales, pero biblioteca es pan o pirámide o cualquier otra cosa, y las siete palabras que la definen tienen otro valor. Tú, que me lees, ¿estás seguro de entender mi lenguaje?).
Jorge Luis Borges
El misterio sigue abierto, e invitamos a los lectores inquietos a disfrutar cuando escriban de ser copartícipes ya sea de un terrible e inescrutable designio o bien de una trivialidad aún no descubierta. C2
Referencias
[Li2013] Li, Wentian, “Characterizing Ranked Chinese Syllable-to-Character Mapping Spectrum: A Bridge between the Spoken and Written Chinese Language” , Journal of Quantitative Linguistics 20 (2): 153-167 (2013).
[Naumis2008] G.G. Naumis, G. Cocho, “Tail universalities as an algebraic problem: the beta-like function”. Physica A 387, 84-96 (2008).
[Petersen2012] A. M. Petersen, H.E. Stanley, S. Succi, “Statistical regularities in the rank-citation profile of scientists”, Science Reports 1, 181, (2012).





Elio Roca Flores -
Gerardo (Naumis, 2008) desarrollo la función (tipo) beta modificada (beta like).
La demostración si es universal es crucial. Como Gerado me explico la gausiana es universal para suma de varialbes aleatorias y la beta modificada para productos de variables a elatorias.
El Tao Te Ching (Preciado, 2012) dice ‘longevidad, tres de cada diez; tres de cada diez, muerte prematura’.
Corrección Pareto por Parteo.
Este artçiculo se puede citar (APA) como:
García Naumis, G. (2017). Leyes de escalamiento en artes y ciencia un enigma aún no resuelto. C2, 28 febrero 2017. https://www.revistac2.com/leyes-de-escalamiento-en-lenguajes-y-ciencia/.
Referencias
Naumis, G. G., & Cocho, G. (2008). Tail universalities in rank distributions as an algebraic problem: The beta-like function. Physica A: Statistical Mechanics and its Applications, 387(1), 84-96.
Preciado Idoreta, I. (2012). Tao Te Ching: Los libros del Tao: Lao Tse.
Monica Mercado -
Me encantó el artículo, nada hay mas sorprendente que la matematica (o estadistica) aplicada. Y seguro esto no es azar porque segun tengo entendido la belleza de las cosas tiene una proporción. Asi que textos, música e incluso la propia la E. coli tiene su propia belleza.