La manera de percibir el espacio y de vivirlo, depende de cada persona.
Para un cazador, el bosque es el lugar donde entiende con mayor claridad los mensajes que le envía su entorno. Mientras está oculto e inmóvil, una rama que de repente se quiebra le indica la presencia de un posible depredador. Pero también hay señales del entorno que sólo alguien con un conocimiento más profundo puede descifrar. Ese cazador interpreta el espacio de acuerdo con su experiencia, y gradualmente ha ido desarrollando una capacidad de decodificación que contribuye significativamente a su desempeño como tal. Para un geómetra el espacio es algo distinto. Desde luego, dependerá de la época y cultura matemáticas en las que vive pues son éstas las que le proporcionan los instrumentos iniciales de conceptualización. Si pensamos en un geómetra griego contemporáneo de Aristóteles (384-322 a.C), por ejemplo, el espacio de su geometría sería una abstracción del espacio físico. Se podría preguntar cómo hacer para determinar la distancia a la que se encuentra un barco de la costa. No le importa si el mar es profundo, si hay mucho oleaje, si el barco es grande o pequeño. Le interesa responder esta pregunta independientemente de estas particularidades. Es decir, le interesa resolver el problema en abstracto, con la confianza de que ese mapa que ha trazado sobre la arena de la playa captura propiedades geométricas esenciales del espacio físico en el que está inmerso. Si le preguntan cómo medir la altura de una pirámide, puede responder de la siguiente manera: Esperemos el atardecer cuando la pirámide proyecte su sombra y apliquemos una semejanza de triángulos. Casi como un mantra: altura de la pirámide dividida entre la sombra de la pirámide igual a estatura del geómetra dividida entre la sombra del geómetra. El único dato desconocido es la altura de la pirámide que se despeja fácilmente de esta proporción: Altura de Pirámide/sombra pirámide = Estatura geómetra/sombra geómetra
La geometría que desarrollaron los griegos fue adquiriendo cada vez más este carácter de modelo exacto del espacio.
Es de hacerse notar que al traducir la situación a un esquema geométrico abstracto y dar respuesta allí al problema traído del mundo material, el geómetra, insistimos, está aceptando que la geometría sobre el papel es un modelo exacto del espacio físico. La geometría era concebida como un guante que al ponerlo sobre la mano, el espacio, la mano y el guante quedan fundidos y no podemos ya distinguirlos uno de otro. La geometría que desarrollaron los griegos a lo largo de varios siglos fue adquiriendo cada vez más este carácter de modelo preciso. Los triunfos que iban acumulando al aplicar el método geométrico a problemas del espacio material iban generando gradualmente tal convicción. Un resultado espectacular se produjo con la medición del radio de la tierra. Vamos a describir someramente la estrategia seguida con ese propósito.
Se sabía que en la ciudad S(Asuán) en un determinado día del año — solsticio de verano— al mediodía, los rayos del sol caían perpendiculares al suelo, lo cual era verificable porque el fondo de un pozo de agua quedaba totalmente iluminado a esa hora. Cuando el fenómeno ocurría en la ciudad S, éste no ocurría en Alejandría. En ésta, si al mediodía de ese mismo día se colocaba una vara perpendicular al piso, se producía una ligera sombra. Eratóstenes (250 a.C), quien vivía en Alejandría extrajo la conclusión correcta: si en S no había sombra y en Alejandría sí, entonces la Tierra no podía ser plana. Si lo fuera y en S no hay sombra es porque los rayos caen perpendiculares al piso plano y así tendría que acontecer en Alejandría. Entonces se planteó el problema de averiguar el tamaño de la tierra que suponía entonces esférica, como la luna, el sol. Para calcular su tamaño debería calcular su radio.

Eratóstenes sabía que la distancia AS entre Alejandría y la ciudad S era de unos 800 kilómetros actuales. Podía suponer que los rayos del sol viajan por rectas paralelas y que así llegan a la Tierra, pues vienen de un punto muy alejado (el sol). Todas estas simplificaciones pertenecen al modelo geométrico de la situación material.
Eratóstenes pudo producir un diagrama como el que ilustra la siguiente figura:
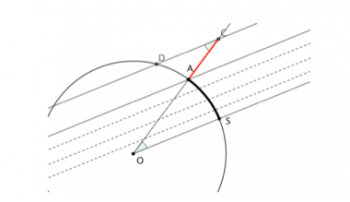
Reiteremos, como los rayos del sol vienen de muy lejos (comparando la distancia entre el sol y la tierra con las distancias que Eratóstenes podía medir sobre la superficie del planeta) podemos suponer que esos rayos son paralelos entre sí. Por lo tanto, al mediodía del día en que se ve iluminado el fondo de un pozo en S, en A(Alejandría) la vara AC produce la sombra AD. Estamos en A y conocemos la distancia D entre las dos ciudades. Esa distancia se puede calcular como el producto cuyos factores son el radio R de la tierra y el ángulo μ que se forma entre los radios OA y OS, Esto es: D=Rμ. En esta expresión conocemos el valor de D y el valor del ángulo μ (que resultó de un poco más que 7 grados) pues este ángulo es el que forman AC y CD. Lograr reproducir el ángulo μ de esta manera fue el toque de genio de Eratóstenes —era como si lo hubiera extraído del centro de la Tierra. El ángulo μ (en el centro de la tierra) y el formado entre AC y CD son iguales porque los rayos de sol son paralelos (una propiedad del modelo matemático) y estos ángulos son alternos e internos entre paralelas y por lo tanto iguales (o congruentes, como también se dice). Con esta idea, Eratóstenes calculó el radio y obtuvo como resultado unos 6,246 kms (que él medía en estadios). El cálculo actual es de 6,371 kms. Tomando en cuenta el complejo de circunstancias históricas entenderemos que es una medición muy aceptable. Este cálculo y todo el diseño de la estrategia involucrada, debió producir una profunda impresión entre los contemporáneos de Eratóstenes; era una prueba más de que la geometría euclidiana reflejaba con certeza la estructura del espacio físico.
La descripción del espacio de Newton iba más allá: era geométrica pero con movimiento.
Siglos después Newton profundizaría mucho más esta convicción al lograr, con su teoría de la gravitación, una matematización casi absoluta del espacio, que ahora se comportaba, plausiblemente, como un mecanismo cósmico. En efecto, su descripción del espacio iba más allá: era geométrica pero con movimiento. Hoy en día diríamos que su modelo era un ejemplo de geometría dinámica. La lectura de los Principia de Newton ofrece una visión del universo construida alrededor de la geometría pero con el ingrediente adicional de la noción de aceleración. Su hipótesis, expresada como la ley universal de la gravitación, adquirió mayor verosimilitud cuando se mostró capaz de recuperar deductivamente las leyes empíricas de Kepler sobre las órbitas planetarias. Los nuevos modelos dinámicos fueron cruciales para inaugurar la entrada plena a las matemáticas de la variación y la acumulación, es decir, aquellas cuyo primer capítulo es el cálculo donde lo discreto y lo continuo encuentran una casa común. El espacio y el tiempo los percibimos como continuos mientras que los números naturales son el paradigma de lo discreto. En el cálculo de Newton, un punto —modelo por excelencia de lo discreto—que se mueve, genera una trayectoria continua. Una vez que el movimiento fue tematizado en las matemáticas, la convicción pitagórica sobre la naturaleza intrínsecamente matemática del universo físico alcanzó su mayor profundidad. Parecía, al decir de sus contemporáneos, que Newton poseía una suerte extraordinaria pues sólo había un universo y a él le correspondió descubrir su estructura oculta.

Las matemáticas parecían incrustadas en la naturaleza como sospechaba Pitágoras y sus seguidores a lo largo de milenios. Ya en esta orilla del tiempo, más cercana a nosotros, recordemos a Fourier, quien solía afirmar que el mundo material era una fuente permanente de inspiración para la creación matemática pues en todo momento legitimaba sus hallazgos. Sin embargo, ya empezaba a cambiar la atmósfera pitagórica y en el texto mediante el cual se comunicaba a Fourier que había obtenido el premio de la academia, se hacía hincapié en la falta de rigor matemático de su trabajo aunque su ecuación (de difusión del calor) era la correcta. Era un Pitágoras un poco más riguroso.
Tendría que pasar un tiempo todavía para que esa convicción de las matemáticas como espejo de la realidad física fuese examinada desde una perspectiva nueva que significaría una profunda ruptura. Por sorprendente que pudiese parecer, la semilla de esa crisis —para emplear el término de Kuhn en su Estructura de las Revoluciones Científicas, FCE, 1971— se encontraba a la vista de todos en los Elementos de Euclides. Nos referimos al postulado de las paralelas. En esencia, este postulado afirma que la paralela que podemos trazar por un punto exterior a una recta dada, en un plano, es única. Como parte de la convicción pitagórica del mundo material, durante más de veinte siglos los geómetras intentaron demostrar la unicidad de la paralela a partir de los restantes postulados euclidianos. La razón para querer demostrarlo como si fuera un teorema más del sistema era que carecía de la evidencia de los restantes postulados.
Por ejemplo, afirmar que por dos puntos pasa una única recta, es algo muy verosímil: basta tensar una cuerda entre nuestras manos para creerlo.
La geometría debía partir de hechos evidentes y, de allí en adelante, el proceso deductivo tendría que encargarse de ir revelando los secretos a los que conducían aquellas primeras intuiciones. Afirmar que la paralela era única no era tan evidente pues se refería al comportamiento de una recta que no podría intersectar a otra dada de antemano, por más que se la prolongara…incluso mucho más allá de donde alcanza nuestra vista. Se perdía pues la evidencia que era tan tangible en los restantes postulados. Todos esos siglos de trabajo no lograron producir una demostración. Era natural pues, que el algún momento alguien llegara a sospechar que aquel aparente fracaso en la búsqueda de una demostración podía deberse a que tal demostración no existía. Fueron Lobachevski y Bolyai, ruso y húngaro respectivamente, quienes de manera independiente rompieron con la convicción que había logrado sobrevivir tanto tiempo, y se atrevieron a pensar en una geometría en donde no se impusiera la unicidad de la paralela por un punto exterior a una recta dada. Si la geometría era como el espejo sobre el que se reflejaba el espacio físico, Lobachevski y Bolyai, fracturaron ese espejo. En su obra Los Nuevos Principios de la Geometría (1825) Lobachevski escribió:
Los sucesivos intentos fallidos por más de dos mil años, desde los tiempos de Euclides, hicieron que se despertase en mí la sospecha de que la verdad que se deseaba probar no estaba contenida en los datos [mismos del problema], y que para establecerla sería necesario recurrir a experimentos, por ejemplo, observaciones astronómicas, como es el caso para otras leyes de la naturaleza.
Lobachevski pone en tela de juicio la naturaleza icónica del sistema euclidiano, es decir, que sea un reflejo especular del espacio físico, como hemos reiterado previamente. Se va haciendo visible la nueva orientación que concibe la geometría como un modelo, como un mapa que no se confunde con el territorio, a saber, el espacio físico. Insistiendo en esta línea de investigación, diez años más tarde (1835) Lobachevski escribe:
Basándome en observaciones astronómicas…verifiqué que en un triángulo cuyos lados son casi tan grandes como la distancia de la Tierra al Sol, la suma de los ángulos difiere de dos rectos en menos de 0.0003 segundos. En consecuencia, puede afirmarse que las proposiciones de la geometría práctica han sido rigurosamente establecidas.
Al concebir esa manera de explorar la naturaleza del sistema geométrico, Lobachevski estaba lanzando un mensaje importante, a saber, que la euclidianidad —si puede decirse así— del sistema heredado de Grecia estaba basado en experiencias del espacio de dimensiones pequeñas, lo que alcanza el ser humano a captar a su alrededor sin ayuda de instrumentos que amplifiquen su percepción. Esa intuición era la que estaba incrustada en el sistema de postulados de Euclides.
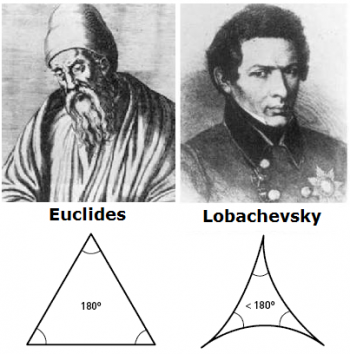 Un triángulo, como el empleado por Lobachevski, podría haber revelado un rasgo geométrico desconocido hasta entonces siempre y cuando la suma de los ángulos de su triángulo hubiera diferido de 180 grados por una cantidad superior al margen del error experimental. Como se sabe, afirmar que la suma de los ángulos internos de un triángulo sea exactamente 180 grados, es una aserción lógicamente equivalente al postulado de las paralelas. Entonces, Lobachevski desafió al sistema euclidiano con su experimento de medición pero su resultado no fue concluyente. Es interesante que él hable de la geometría euclidiana como práctica; se puede presentir que tenía clara la diferencia entre el sistema formal, organizado alrededor de los postulados y la adecuación del sistema como modelo del espacio físico.
Un triángulo, como el empleado por Lobachevski, podría haber revelado un rasgo geométrico desconocido hasta entonces siempre y cuando la suma de los ángulos de su triángulo hubiera diferido de 180 grados por una cantidad superior al margen del error experimental. Como se sabe, afirmar que la suma de los ángulos internos de un triángulo sea exactamente 180 grados, es una aserción lógicamente equivalente al postulado de las paralelas. Entonces, Lobachevski desafió al sistema euclidiano con su experimento de medición pero su resultado no fue concluyente. Es interesante que él hable de la geometría euclidiana como práctica; se puede presentir que tenía clara la diferencia entre el sistema formal, organizado alrededor de los postulados y la adecuación del sistema como modelo del espacio físico.
Esta idea que hemos comentado repetidamente, que un sistema matemático es sólo un modelo, o un mapa, todavía no estaba madura. Justamente esa idea va a desarrollarse, en gran medida, a partir del trabajo pionero de Lobachevski y Bolyai —a quien aquí sólo hemos mencionado de pasada aunque su trabajo tiene tanta importancia como la que corresponde al geómetra de Kazán.
El problema que aquí hemos intentado explicar constituye uno de los momentos más significativos de las matemáticas modernas.
El problema que aquí hemos intentado explicar constituye uno de los momentos más significativos de las matemáticas modernas. La des-sustanciación de los sistemas formales de las matemáticas, es decir, la distinción entre sistema formal y modelo, ha sido de una importancia que no se puede exagerar. Puede afirmarse sin titubeos que la epistemología de las matemáticas sufrió, con la creación de las geometrías no-euclidianas, una transformación que llega hasta nuestros días. No es un problema del pasado, como no lo es la teoría de la evolución, más bien son elementos transformadores del concepto mismo de conocimiento científico. Son esos hombros de gigantes a los que se refería Newton mientras paseaba por las playas buscando los más bellos guijarros. C2




Rosa M Herrera -
Este es uno de esos artículos de C2 que leo dos veces en la segunda me recreo, me interesa el tema, me gusta el enfoque, me parece que los lectores disfrutarán tanto aquellos cercanos al ambiente en que se enmarca, como los ajenos. Esperemos que la saga continúe.