Del cómputo cuántico y de sus universos paralelos. Parte 1

Ciencia

Del cómputo cuántico y de sus universos paralelos. Parte 1

5 septiembre, 2017
|
POR Francisco Rodríguez Henríquez
|
0 COMENTARIOS
|
Like 0
|
1,001

“Paracelso dijo con lentitud:
– El camino es la Piedra. El punto de partida es la Piedra. Si no entiendes estas palabras,
no has empezado aún a entender. Cada paso que darás es la meta.”
“La rosa de Paracelso”, Jorge Luis Borges.

En mayo de 1981 Richard Feynman escribió un artículo que con los años se volvería muy famoso, con uno de los títulos más provocativos de todos los tiempos para un trabajo científico (o literario): Simulating Physics with Computers, en el cual se plantea la posibilidad de imitar a la naturaleza mediante la construcción de una computadora capaz de explotar dos de los principios físicos fundamentales de la mecánica cuántica, la superposición y el entrelazado de estados en partículas elementales [1]. Feynman concibió que la información a ser procesada por ese artefacto estaría contenida en unidades de memoria conformadas por partículas elementales, y sugirió utilizar partículas de Bose y Fermi para tales fines. En el último párrafo de su artículo-ensayo Feynman escribió:

“[…] And I’m not happy with all the analyses that go with just the classical theory, because nature isn’t classical, dammit, and if you want to make a simulation of nature, you’d better make it quantum mechanical, and by golly it’s a wonderful problem, because it doesn’t look so easy” [2].

Y más de treinta y seis años después podríamos contestarle al profesor Feynman que sí, que efectivamente, que yes indeed, que lograr fabricar las primeras computadoras cuánticas ha sido un proyecto nada fácil.

En esta nota se presentan los principales hitos científicos y tecnológicos alcanzados hasta ahora en el desarrollo de esta ambiciosa empresa, la cual varios grupos de investigación importantes aseguran que están a punto de culminar con el anuncio de sus primeros éxitos concretos, pero que otras voces en la comunidad científica siguen viendo con un escepticismo mal disimulado.

Comenzamos nuestra descripción presentando a los inefables qubits.

Sobre los qubits y sus extraños efectos cuánticos

Para aquellos de entre nosotros que no somos versados en mecánica cuántica, pero que sí recibimos en nuestra remota juventud una introducción competente a la física moderna (en mi caso especialmente competente, pues tuve el honor de tomar todas mis clases de física y de cálculo a nivel licenciatura con el Profesor Gerardo Torres del Castillo en la Facultad de Físico Matemáticas de la Universidad Autónoma de Puebla). Aprendimos con el tiempo y con cierta práctica, a recitar con soltura frases famosas, enunciadas en otras épocas por físicos alemanes o austríacos. Frases tales como la einsteniana: “obedeciendo al principio de dualidad, la luz es tanto onda como partícula”, o la schrödingeriana: “el gato no está vivo ni tampoco muerto hasta que se le observa”, o la heisenbergiana: “podemos saber la posición o el momentum de una partícula, pero no ambos al mismo tiempo”, o la sorpresiva: “una partícula instantáneamente averigua el spin de la otra a través de una siniestra acción que opera a la distancia”, la cual, se sabe, provocó grandes recelos en el propio Einstein. Sin embargo, en nuestro fuero interno sabíamos y sabemos, como quien dice, a ciencia cierta, que la física detrás de estos estribillos sólo podría aprenderse (y aprehenderse) a través de un arduo esfuerzo en largos años de estudio.

La unidad de memoria digital por antonomasia es el humilde bit.

En este artículo estamos interesados en exponer algunos detalles interesantes y sorprendentes sobre el cómputo cuántico, una de las aplicaciones más fascinantes de la física de la mecánica cuántica, y en donde esta teoría centenaria se reúne armoniosamente con otra no menos bella e intrincada (pero mucho más joven): la teoría de la complejidad computacional [3]. Para nuestros propósitos, nos limitaremos a asomarnos de puntillas a la mecánica cuántica vista como una generalización de la teoría clásica de la probabilidad, tomándonos la libertad, como se verá a continuación, de utilizar valores negativos para describir estados probabilísticos. Iniciamos nuestra explicación estudiando con cuidado lo que ocurre con la unidad de memoria digital por antonomasia: el humilde bit.

Bits y qubits

En la teoría de la probabilidad clásica, un bit puede ser descrito como una unidad de memoria que tiene una probabilidad p de estar en un valor 1 y una probabilidad 1-p de estar en un valor cero. En notación vectorial esta observación implica que un bit puede ser representado como el vector (p, 1-p), donde p es un número real positivo menor que 1. En este caso se dice que la norma-1 del vector bit, definida como la suma de los valores absolutos de las entradas de éste, debe ser igual a uno. De manera más general, consideremos el caso de un registro clásico compuesto por n bits. Esta unidad de memoria puede representar hasta N = 2ⁿestados diferentes, pero en un mundo clásico, sólo uno de estos N valores puede estar almacenado en el registro en un momento dado. Por ejemplo, para n = 3, los ocho posibles valores binarios que un registro de tres bits puede representar son:

E₀ = 000; E₁ = 001; E₂ = 010; E₃ = 011; E₄ = 100; E₅ = 101; E₆ = 110; E₇ = 111.

Si no se conoce a priori el estado de este registro, entonces las probabilidades de que en un momento dado ocurra alguno de estos ocho posibles estados, puede ser descrito con un vector de N entradas, (p₀, …, p_N_-1), donde todos los valores p_i para i = 0,…, N-1, son números reales positivos cuya suma debe ser igual a uno, y donde la probabilidad de que el registro de n bits se encuentre en un cierto momento en el estado i-ésimo, está dado por p_i. En el mundo clásico, de manera crucial, se considera que el estado (uno o cero) de un determinado bit no tiene porqué observar ninguna correlación con los valores que se encuentren en esos momentos almacenados en ninguno de sus bits vecinos. En contraste, como se explica más adelante, los qubits de un registro cuántico sí tienen la costumbre de interactuar (si bien es cierto que por un brevísimo tiempo) entre sí.

Regresando a la norma-1, esta no es la única norma en el mundo matemático. En particular, desde los antiguos tiempos de Pitágoras ya se conocía la norma-2 o norma euclidiana.

Si ahora decidimos representar a un vector bit utilizando la norma-2, entonces el nuevo requisito es que la suma de los cuadrados de dos números sea igual a uno. De esa manera, un vector bit de norma-2 queda descrito como (α, β) tal que, α² + β² = 1. Si se permite además que α, β sean números complejos, ocurre que un vector bit de norma-2 describe con precisión el comportamiento de un qubit, el cual es una apócope para quantum bit.

En física se prefiere utilizar la notación de Dirac, en la cual el vector (α, β) se escribe como: α|0> + β|1>. La base computacional para describir los estados de un qubit está dada como: |0> = (1, 0)^T, y |1> = (0, 1)^T.

Efectos cuánticos

Utilizando matrices unitarias de dimensión 2×2, es posible transformar los estados de un qubit, produciendo un efecto conocido como interferencia cuántica. Por ejemplo, considérese la siguiente matriz unitaria (Ecuación 1):

la cual en una interpretación geométrica toma un vector en el plano cartesiano y la rota 45 grados en contra de las manecillas del reloj. Si aplicamos la matriz unitaria H a un qubit en estado |0> = (1, 0)^T, se obtiene la ecuación 2:

el cual puede ser interpretado como el estado que representa al evento de tirar una moneda al aire. Sin embargo, si aplicamos nuevamente la transformación unitaria H, se obtiene el estado |1>, pues (Ecuación 3):

Esto implica que, mediante la aplicación sucesiva de matrices unitarias, es posible llevar a un qubit desde un estado de superposición dado por la ecuación 2 a un estado determinista dado por |1>. En la práctica, las matrices unitarias son implementadas como compuertas cuánticas.

De nuestro conocimiento de circuitos clásicos sabemos que en el caso de circuitos lógicos booleanos se puede definir un conjunto universal de compuertas lógicas que permiten realizar cualquier función booleana arbitraria. Por ejemplo, las compuertas lógicas AND y NOT, o incluso las compuertas NAND, son conjuntos universales de compuertas en el mundo clásico. Por su parte, en el mundo cuántico existen también varios conjuntos universales de compuertas, siendo uno de los más famosos, el conjunto conformado por la compuerta Hadamard junto con la compuerta Toffoli.

De enredos y desenredos

En el cómputo cuántico: ¿cómo se interpretaría un registro de n qubits? En particular, tal y como ocurre en el mundo clásico: ¿son los estados almacenados por qubits independientes entre sí? La respuesta a esta última pregunta es un rotundo (y sorprendente) ¡no!

Ciertamente, además del efecto de superposición ya descrito anteriormente, las computadoras cuánticas intentan tomar ventaja del efecto de entrelazado cuántico (entanglement en inglés) entre los qubits. En un escenario ideal, todos los qubits de una computadora cuántica deberían estar entrelazados o enredados entre sí. De esa manera, cuando se aplica una compuerta cuántica en algunos de los qubits, también se estarían afectando simultáneamente a todos los otros qubits.

Recapitulemos lo estudiado hasta el momento: Un qubit puede entonces estar en el estado cero, en el uno, o en cualquier superposición cuántica de estos dos estados. Una pareja de dos qubits puede estar en superposición de cuatro estados, y en general, un registro cuántico de n qubits, puede estar en una superposición arbitraria de hasta N = 2ⁿ estados simultáneamente. En contraste, como se mencionó anteriormente, un registro clásico de n bits puede estar en tan sólo uno de esos N estados. Un registro cuántico puede ser manipulado a través de compuertas cuánticas como las descritas anteriormente y en tanto todos los qubits de dicho registro estén entrelazados, entonces las manipulaciones que sufra un subconjunto de los qubits en el registro serán sufridas por todos los qubits que estén enredados entre sí.

De decoherencias e incoherencias

La secuencia exacta en la que las compuertas cuánticas son aplicadas sobre el registro de qubits define el algoritmo cuántico que está siendo ejecutado, en donde se toma al estado inicial del registro como los datos de entrada del procedimiento. El algoritmo finaliza cuando el sistema cuántico de n qubits colapsa a uno de los N posibles estados clásicos, es decir, cuando se tiene que cada uno de los n qubits alberga un valor determinístico que es ya sea cero o uno. Decimos entonces que los qubits del registro cuántico no se encuentran ya en superposición, sino que más bien éstos han alcanzado el estado de decoherencia (decoherence en inglés), arrojando a su salida n bits clásicos de información.

En la práctica, los algoritmos cuánticos suelen ser probabilísticos, en el sentido de que ellos obtienen la solución correcta al problema investigado tan solo con una cierta probabilidad de certidumbre estrictamente menor que uno. Debido a ello, típicamente los algoritmos cuánticos deben ser re-ejecutados muchas veces para poder tener una confianza razonable de haber hallado la respuesta correcta. Por ejemplo, si un determinado algoritmo cuántico encuentra una solución a un problema de decisión (esto es, problemas cuya salida es sí o no, tales como determinar si acaso un número positivo n es primo o no), con probabilidad de 2/3, entonces el procedimiento deberá re-ejecutarse un número grande de veces, de tal manera que si se obtiene la misma respuesta en k experimentos distintos, la probabilidad de que el algoritmo en verdad tomó la decisión correcta estaría dada por 1-(2/3)^k.

En la naturaleza, las partículas que se encuentran en estado cuántico de superposición tienden, a la menor provocación, a colapsarse al estado de decoherencia. En muchos sentidos, esto es un hecho muy afortunado, pues de otra manera contemplaríamos en nuestra vida cotidiana los extravagantes efectos de la superposición en la que muchos estados cuánticos estarían ocurriendo al mismo tiempo. Ciertamente, sería un mundo sumamente extraño, muy distinto al que nos tocó vivir.

Por otro lado, para propósitos de diseño y fabricación de computadoras cuánticas, uno de los principales quebraderos de cabeza, y acaso el principal, es cómo lograr que los registros de qubits se mantengan en estado de superposición por un tiempo lo suficientemente grande como para que se puedan aplicar sobre ellos las transformaciones de las compuertas que realizan la ejecución del procedimiento cuántico, antes de que ineludiblemente los qubits decaigan al estado de decoherencia. Por lo general se necesita que las compuertas cuánticas sean unas diez mil veces (≈2¹³) más rápidas que el tiempo de decoherencia. Y dependiendo de la tecnología y del número de qubits, el estado de superposición operando a bajísimas temperaturas puede prolongarse algunos cientos de nanosegundos.

Las computadoras cuánticas de la compañía D-Wave trabajan a menos de un grado Kelvin.

En efecto, intuitivamente la mejor manera de maximizar el tiempo en que el estado de superposición campea entre los qubits, es la de intentar que éstos estén cuidadosamente aislados del mundo exterior. Por ello, los artefactos cuánticos construidos hasta ahora operan en temperaturas extremadamente bajas. Por ejemplo, las computadoras cuánticas de la compañía D-Wave trabajan a menos de un grado Kelvin. Varias de las topologías sugeridas para otros diseños de artefactos cuánticos requieren que éstos operen a una temperatura de unos 20 mili-grados Kelvin, literalmente rozando el cero absoluto, como único recurso para evitar una decoherencia masiva que evitaría realizar cómputo útil con compuertas cuánticas [4].

Aun con los más primorosos cuidados, resulta imposible evitar que la decoherencia ocurra en algunos de los qubits, lo cual provoca que la valiosa información que está presente por decirlo así, de una manera virtual en los estados en superposición, se pierda. Una técnica que resuelve este inconveniente utiliza una corrección quántica de errores, lo cual implica que se vuelve necesario diseñar qubits redundantes cuya única misión es la de corregir los errores producidos por la decoherencia observada en otros qubits que transportan información. Esta situación es un verdadero problema, pues la corrección cuántica podría ser tanto o más cara (medida en número de qubits asignados a esta tarea), que el propio cómputo que se desea calcular.

Un ejemplo ilustrativo ocurre con la ejecución del célebre algoritmo de Shor para factorización de números enteros grandes. Este famoso algoritmo puede factorizar números gigantes en tiempo polinomial, a un costo de entre n a n² qubits, donde n es el tamaño en bits del número a ser factorizado. Sin considerar la corrección de errores, se estima que un número de 1000 bits podría ser factorizado utilizando una computadora equipada con aproximadamente 2¹³ qubits. Sin embargo, si se considera el gasto extra incurrido por el mecanismo de corrección de errores, la cantidad se eleva a 2²³ qubits. Debido a estas consideraciones, existe consenso en la comunidad de cómputo cuántico en que las aplicaciones criptográficas (como lo es la implementación del algoritmo de Shor), son de las más complejas y desafiantes de entre las aplicaciones del mundo real sugeridas para este paradigma.

Figura 1. Circuito integrado presente en la computadora cuántica de Google [imagen tomada de Internet]

Supremacía cuántica

Dado que un registro de n qubits puede estar en una superposición arbitraria de hasta N = 2ⁿ estados diferentes, y que las probabilidades individuales de cada qubit son expresadas como números complejos, una computadora clásica necesita una cantidad de memoria mayor a 2ⁿ bits para poder representar los posibles estados que puede tomar una computadora cuántica equipada con n qubits [5].

Es esta observación la que permite afirmar que las computadoras cuánticas ofrecen una aceleración exponencial con respecto a una computadora clásica.

Para poner esta propiedad en perspectiva, piénsese en una computadora cuántica equipada con 8 qubits. Una simulación clásica de este artefacto requeriría de una computadora convencional con al menos 2⁸ = 256 bits, con los cuales a su vez se pueden representar hasta 2²⁵⁶ valores diferentes. Si se considera una computadora cuántica equipada con 50 qubits, entonces sería necesario disponer de una computadora clásica con una capacidad de memoria de al menos 2⁵⁰ bits, es decir 1 Peta bit, lo cual es un tamaño de memoria al alcance únicamente de los más poderosos servidores actuales. Si se piensa ahora en una computadora cuántica equipada con 80 o más qubits, su simulación en computadoras convencionales exigiría una capacidad de cómputo muy superior a la súper computadora clásica más poderosa construida hasta el día de hoy. De hecho, no está para nada claro que una computadora clásica con una memoria de 2⁸⁰ bits pueda jamás ser construida.

La supremacía cuántica se define como la aceleración que puede alcanzarse usando cómputo cuántico para resolver una tarea útil que sea computacionalmente intratable aun para las más poderosas súper computadoras clásicas. La competencia para demostrar por primera vez supremacía cuántica se ha vuelto una carrera muy apretada entre los gigantes de la informática Google e IBM.

IBM anunció en mayo de este año que cuenta ya con el prototipo de una computadora universal cuántica.

John Martinis, líder del grupo de investigación cuántica de Google, cree que la supremacía cuántica puede alcanzarse fabricando una computadora con tan solo 49 qubits (en la figura 1 se muestra un circuito integrado de la arquitectura de esta computadora). Martinis considera además que su equipo de investigación será capaz de producir este resultado antes de que termine este año [6]. Por otra parte, el grupo de investigación cuántica de IBM anunció en mayo de este año que cuenta ya con el prototipo de una computadora universal cuántica, llamada IBM Q, el cual está equipado con 17 qubits. Ellos esperan poder alcanzar la supremacía cuántica en los próximos años, mediante el escalamiento de su prototipo a un artefacto equipado con 50 qubits. Una característica importante de IBM Q es que desde el principio sus diseñadores se plantearon el reto de construir una computadora cuántica con capacidades de ser programada para ejecutar diferentes algoritmos (característica que generalmente no está presente en sus competidores). Finalmente, no podemos dejar de mencionar en este apartado a la compañía canadiense D-Wave, cuyos voceros han afirmado durante toda lo que va de esta década, haber alcanzado supremacía cuántica con una computadora del tipo recocido simulado que de acuerdo con sus datos estaría equipada con más de 1000 qubits.

Sin embargo, los investigadores de estos grupos reconocen que la inminente supremacía cuántica que estiman poder anunciar en los próximos años, sería únicamente alcanzada para aplicaciones más bien artificiales y planeadas adhoc en condiciones ideales de laboratorio. Aunque las opiniones suelen variar mucho, en general existe consenso en que las aplicaciones del cómputo cuántico en problemas del mundo real requieren por lo menos una década más de desarrollo de la ciencia y la tecnología de esta disciplina [7].

Topologías propuestas para la construcción de computadoras cuánticas

En la actualidad, existen cuatro modelos de importancia práctica para el desarrollo de computadoras cuánticas:

Arreglos de compuertas cuánticos. En esta topología la ejecución de algoritmos consiste en la ejecución de una secuencia de compuertas cuánticas.
Computadora cuántica de sólo-ida. En este modelo los cálculos son una secuencia de mediciones de qubits aplicados sobre registros cuánticos altamente enredados
Simuladores cuánticos (también conocidos como computadoras cuánticas adiabáticas). Esta topología hace uso del algoritmo de recocido simulado ejecutado cuánticamente. Este modelo se caracteriza por no ser reprogramable para la ejecución de diferentes procedimientos, y es el modelo más apegado a la concepción original que Feynman formulara en 1981.
Computadora cuántica topológica. En este caso el cálculo está compuesto por una retícula de aniones en dos dimensiones, las cuales son unas partículas que prometen un efecto de superposición mucho más estable. Este es el modelo adoptado por el grupo de investigación cuántica de Microsoft.

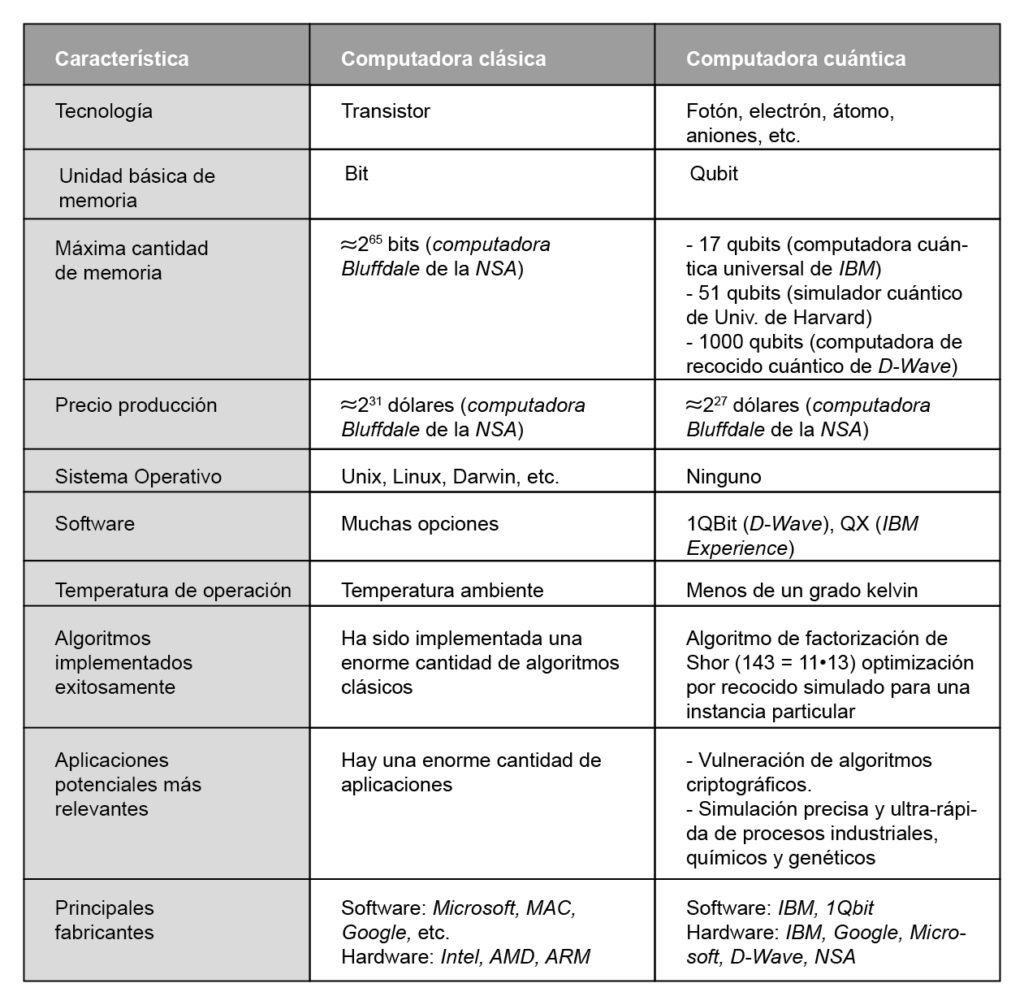
La tabla 1 muestra un comparativo a nivel lógico, tecnológico y funcional de los paradigmas de cómputo clásico y cuántico.

Tabla 1. Cuadro comparativo entre computadoras clásicas y cuánticas.

Figura 2. Vistas interiores de la computadora cuántica de D-Wave [imágenes tomadas del sitio web de la compañía]

La verdad en el caso de la compañía cuántica D-Wave

Desde hace una década, la compañía canadiense en desarrollo D-Wave presume de haber producido computadoras adiabáticas, las cuales realizan simulaciones cuánticas del algoritmo de recocido simulado. Los anuncios de D-Wave han causado mucha polémica en la comunidad científica que hasta la fecha se muestra muy escéptica sobre tales afirmaciones. Muy particularmente, el debate se centra sobre si en verdad en las computadoras de D-Wave se alcanzan a observar los efectos de superposición y de entrelazado. Parte de este recelo cedió cuando un grupo de investigadores de esta compañía publicó en el 2011 un artículo en Nature donde quedó demostrado que después de todo, su computadora sí alcanzaba el fenómeno de entrelazado cuántico. En la arquitectura de las computadoras de D-Wave, los qubits están dispuestos en registros de 8 qubits que observan un alto grado de enredamiento. La compañía presume que su computadora más poderosa, la D-Wave 2X que fuera anunciada en agosto de 2015, está equipada con más de 1000 qubits (véase la figura 2 y la Tabla 1).

La cartera de clientes de la compañía D-Wave incluye una impresionante lista de grandes trasnacionales tales como: Lockheed Martin, Google, Volkswagen, etc. Así como colaboraciones con agencias gubernamentales tales como la NASA y The Alamos Labs.

A pesar de todos estos éxitos científicos y comerciales, las dudas persisten. En todo caso, está claro que D-Wave está a la cabeza del desarrollo de la tecnología que deberá acompañar a una computadora cuántica. Muy particularmente, en el desarrollo de congeladores capaces de proveer ambientes controlados ultra fríos con temperaturas menores a un grado Kelvin.

Continua Parte 2

Referencias

[1] El concepto de computadoras cuánticas fue propuesto previamente en 1980 por Paul Benioff y Yuri Manin.

[2] “Y a mí no me hacen gracia todos esos análisis que están fundamentados únicamente en la teoría clásica, porque, ¡diablos!, la naturaleza no es clásica, y si en serio quieres hacer una simulación de la naturaleza, debes asegurarte de hacerla con mecánica cuántica, y vaya que sí es un problema maravilloso, porque no luce nada sencillo” [traducción libre del autor].

[3] Las formulaciones iniciales de la mecánica cuántica surgieron en los primeros años del siglo XX. En cambio, los estudios sistemáticos de la teoría de la complejidad computacional comenzaron a mediados de la década de los sesentas del siglo pasado. Es así como mientras la mecánica cuántica es una disciplina con más de cien años de existencia, la teoría de la complejidad computacional es apenas una ciencia cincuentona.

[4] Sin embargo, el año pasado se demostró experimentalmente que el spin de electrones puede ser observado por alrededor de 175 nanosegundos a temperatura ambiente. Esto es un pequeño pero alentador paso hacia la posible construcción de computadoras cuánticas a temperatura ambiente

[5] Más precisamente, se necesitaría que los recursos de memoria de una computadora cuántica permitieran almacenar 2ⁿ números complejos para poder así simular clásicamente a todos los posibles estados que una computadora cuántica de n qubits puede tomar.

[6] Sin embargo, es importante señalar que esta supremacía computacional se alcanzaría en el cómputo de una tarea muy específica. En particular, el artefacto cuántico diseñado por Google no sería reprogramable, por lo que no podría ejecutar ningún otro algoritmo.

[7] Aunque sigue habiendo voces importantes en la Física que afirman que una verdadera computadora cuántica jamás será construida. El principal argumento de su escepticismo es cómo resolver la cuestión de lograr una corrección cuántica que mitigue eficientemente la pertinaz decoherencia.