Todos sabemos que si rotamos un recipiente lleno de un líquido (agua por ejemplo), su superficie adquiere un perfil parabólico.

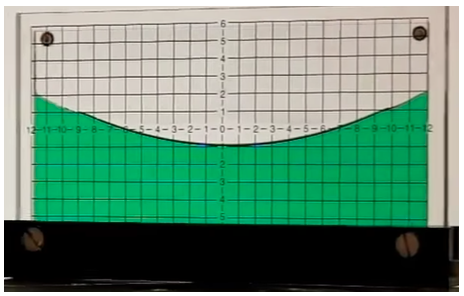
En sus Principia, Newton describe el experimento del cubo rotante: llena un cubo con agua y lo ata a una cuerda, que luego enrolla hasta que se vuelve rígida. Luego suelta el cubo, que comienza a descender y girar. Al principio solo gira el cubo, mientras que el agua permanece estacionaria y su superficie horizontal (incluso si hay olas). Luego, lentamente, debido a su viscosidad, el agua también comienza a girar y su superficie adquiere la típica forma parabólica. Una vez que la cuerda está completamente desenrollada, comienza a rebobinarse en la dirección opuesta y el cubo se eleva, lo que ralentiza su rotación. Sin embargo, durante un tiempo, el agua sigue girando en el mismo sentido que antes, siempre con la superficie parabólica, y se detiene mucho después de que el cubo lo haya hecho.

If a vessel, hung by a long cord, is so often turned about that the cord is strongly twisted, then filled with water, and held at rest together with the water; after, by the sudden action of another force, it is whirled about in the contrary way, and while the cord is untwisting itself, the vessel continues for some time this motion; the surface of the water will at first be plain, as before the vessel began to move; but the vessel by gradually communicating its motion to the water, will make it begin sensibly to revolve, and recede by little and little, and ascend to the sides of the vessel, forming itself into a concave figure…This ascent of the water shows its endeavour to recede from the axis of its motion; and the true and absolute circular motion of the water, which is here directly contrary to the relative, discovers itself, and may be measured by this endeavour. … And therefore, this endeavour does not depend upon any translation of the water in respect to ambient bodies, nor can true circular motion be defined by such translation. …; but relative motions…are altogether destitute of any real effect. …It is indeed a matter of great difficulty to discover, and effectually to distinguish, the true motions of particular bodies from the apparent; because the parts of that immovable space in which these motions are performed, do by no means come under the observations of our senses.
Isaac Newton; Principia, Libro 1: Scholium

Newton concluye que no es la rotación del cubo lo que causa la forma parabólica de la superficie del agua, sino el hecho de que el agua gira. Pero, y aquí viene el problema principal, ¿rotar con respecto a qué [2]?

En el caso de los movimientos de traslación, Galileo ya había señalado que no se puede hablar de velocidad absoluta y, por tanto, que todos los sistemas inerciales son equivalentes. Pero esto no es cierto para las rotaciones: el experimento del cubo muestra que uno puede distinguir experimentalmente entre sistemas rotantes y estacionarios, con respecto a un sistema de referencia que Newton toma en las estrellas fijas. Entonces, hay un sistema o al menos una clase de sistemas de referencia privilegiados. A menos que, al girar las estrellas fijas y mantener inmóvil el cubo, se produzca la misma elevación parabólica del agua … Pero, por supuesto, este es un experimento imposible.

Sin embargo, Mach, 200 años después, considera precisamente este punto al afirmar que los sistemas de referencia deben necesariamente estar conectados a masas y, por lo tanto, depender de ellas [3].

Newton’s experiment with the rotating vessel of water simply informs us that the relative rotation of the water with respect to the sides of the vessel produces no noticeable centrifugal forces, but that such forces are produced by its relative rotations with respect to the mass of the earth and other celestial bodies.
Ernst Mach, as quoted by L. Bouquiaux in Leibniz, p. 104

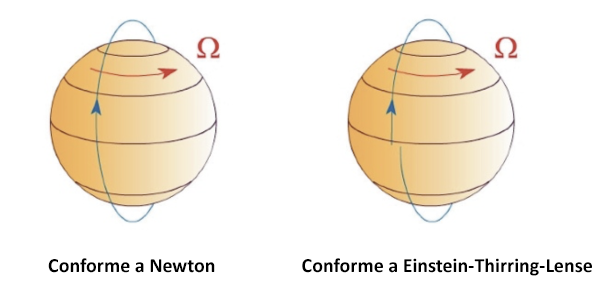
El análisis machiano [4] influye en Einstein, quien en la teoría de la relatividad general establece el principio de equivalencia entre masa inercial y masa gravitacional, estableciendo prácticamente la indistinguibilidad entre inercia y fuerzas gravitacionales. Entonces, al principio, podría tomar una esfera hueca de gran masa, cerrar un balde con agua dentro y ponerlo en rotación. El agua del cubo debe adoptar un perfil parabólico.

De hecho, en 1918 dos físicos austriacos, Hans Thirring y Josef Lense demostraron que la relatividad general de Einstein resuelve el problema: una masa en rotación arrastra el espacio con ella (arrastre de cuadros) dando lugar a una especie de vórtice, de modo que un cuerpo que si cae sobre esta masa no seguiría una línea recta sino una especie de espiral [5].

En la película “Interestelar” la imagen de Gargantúa se construyó teniendo en cuenta este arrastre, que obviamente también afecta a la luz [6].

¿Pero todo esto sucede en realidad? Sí, los experimentos realizados en 2004 por Ciufolini y Pavlis sobre las variaciones orbitales de dos satélites, y repetidos con el experimento “Gravity Probe B”, muestran que la Tierra también arrastra el espacio-tiempo durante su rotación.

Volviendo a Newton, lo que distingue las rotaciones a velocidad constante de las traslaciones siempre a velocidad constante son las aceleraciones: en una rotación, un cuerpo se acelera incluso si gira a una velocidad constante (angular), porque la velocidad del vector, aunque permanece constante en magnitud, siempre cambia de dirección.

El principio de equivalencia de Newton se ilustra a menudo usando un cohete que puede acelerar con la aceleración g, o que puede estar en reposo en la superficie de un planeta de manera que su aceleración debida a la gravedad es –g. En el sistema de referencia del cohete acelerado, en un cuerpo de masa (inercial) m hay una fuerza (“aparente”) de inercia , -mg mientras que en el planeta el cuerpo de masa (gravitacional) m siente una fuerza (gravitacional) -mg. El principio de equivalencia dice que ningún experimento puede distinguir entre estas dos fuerzas, por lo que las dos masas son idénticas por una ley de la naturaleza y no por coincidencia. La equivalencia conduce a la consecuencia inmediata de la desviación de la luz por un campo gravitacional.

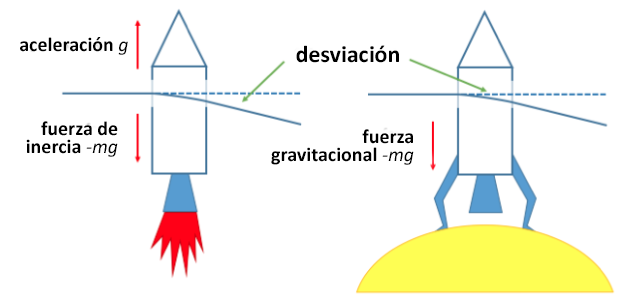
Ahora suponga que el planeta en el que descansa el cohete comienza a acelerar alejándose del cohete. En los primeros momentos, la distancia entre el planeta y el cohete no ha cambiado, por lo que la fuerza gravitacional es la misma. Pero si el cohete y el planeta son los únicos objetos en el universo, el efecto debe ser el mismo que cuando el cohete acelera para despegar del planeta. En este caso, sin embargo, además de la fuerza gravitacional, también se debe sentir una fuerza de inercia. Según el principio de equivalencia, las dos situaciones son indistinguibles, por lo que las masas aceleradas (el planeta) deben generar fuerzas adicionales, debido al arrastre del espacio-tiempo.

En esta aproximación el efecto no depende de la distancia entre el planeta y el cohete, porque es esencialmente el cambio de sistema de referencia. Obviamente, insertando las ecuaciones de Einstein lo que sucede es que la aceleración del planeta genera una perturbación gravitacional que se propaga a la velocidad de la luz.

Ahora consideramos el caso de una esfera que gira alrededor de un cubo y estudiamos que pasa a una porción de agua de masa m que no está en el centro del cubo.

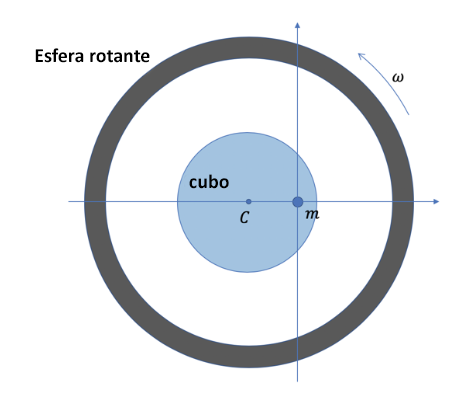
Tomemos un sistema de referencia centrado en m, de manera que con respecto a este la esfera gire con velocidad angular ω de manera excéntrica ya que la masa no está en el centro del cubo.

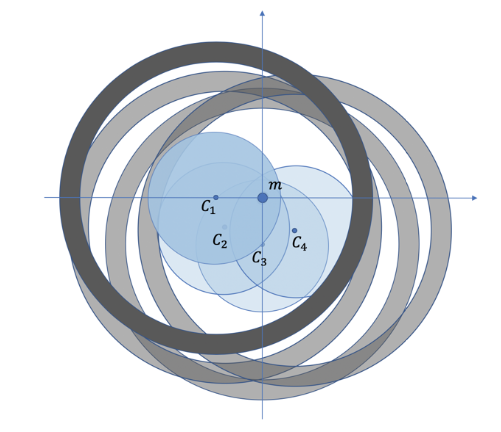
La parte de la esfera más cercana a m acelera hacia ella, luego la empuja hacia el centro, pero la parte más lejana (por lo tanto con mayor aceleración relativa) la empuja hacia la periferia. Dado que la fuerza centrífuga depende linealmente de la distancia, el efecto general de la esfera es el mismo si toda su masa se concentrara en el centro, que “orbita” alrededor de m. Entonces, la aceleración general de la esfera con respecto a m se dirige hacia afuera y es igual a la fuerza centrífuga (dividida por m) que siente la porción de agua en el marco donde la esfera está estacionaria y ella gira.

Quién sabe si Mach habría quedado satisfecho con mi explicación. C²

 

Referencias

1. Jeff Regester, Spinning Water: The Experiment, 2012 (YouTube) https://youtu.be/RdRnB3jz1Yw
2. Bucket Argument (Wikipedia) https://en.wikipedia.org/wiki/Bucket_argument
3. Richard Staley, Ernst Mach on bodies and buckets, Physics Today 66, 12, 42 (2013); doi: 10.1063 / PT.3.2214 https://physicstoday.scitation.org/doi/pdf/10.1063/PT.3.2214
4. Principio de Mach (Wikipedia) https://en.wikipedia.org/wiki/Mach%27s_principl
5. frame dragging (Wikipedia ) https://en.wikipedia.org/wiki/Frame-dragging
6. Kip Thorne, The Science Of Interstellar, New Directions, 2014. Isbn 978-0393351378
7. David Eckstein, Epstein Explains Einstein, epubli GmbH Berlín, epubli.de

---

• (2013). Isbn 978-3844270600
• https://www.epubli.de/shop/buch/Epstein-Explains-Einstein-David-Eckstein-9783844270600/31227

• 0 COMENTARIOS
• |
• VER COMENTARIO