La mirada inicial del Sistema Solar nos proporciona una imagen de un mecanismo bien organizado, con todos sus engranajes funcionando con precisión que, aparentemente al menos, es casi perfecto.
Esta visión pictórica (y algo simplificada) es bastante útil para muchos propósitos relacionados con el conocimiento de nuestro sistema planetario. En una observación algo más atenta, la estructura armónica de cuerpos en interrelación nos muestra, en efecto, que tras un largo proceso ésta ha logrado alcanzar una situación de equilibrio dinámico relativo.
Veamos cómo se puede expresar la idea de manera que resulte útil para obtener información de nuestro sistema planetario y una mayor comprensión del mismo.
¿Es el número de equilibrios relativos entre los cuerpos finito, para cualquier conjunto de masas?
Un equilibrio relativo en el Sistema Solar se corresponde con una solución de las ecuaciones de Newton originada por un movimiento de giro en un plano. Dado que en nuestro sistema planetario se producen numerosas situaciones de este tipo nos preguntamos: ¿es el número de equilibrios relativos entre los cuerpos finito, para cualquier conjunto de masas m1 m2…mn?
Así mismo, alguien podría plantear la siguiente pregunta: ¿sería posible ubicar un cuerpo en una posición cualquiera en nuestro sistema planetario, de manera que sea estable o relativamente estable?
Los puntos de Lagrange
El modelo matemático que estudia la dinámica del Sistema Solar se denomina problema de los n cuerpos y es un problema sin solución analítica. Sin embargo, para algunos casos en que n = 3 es posible obtener una buena descripción del movimiento.
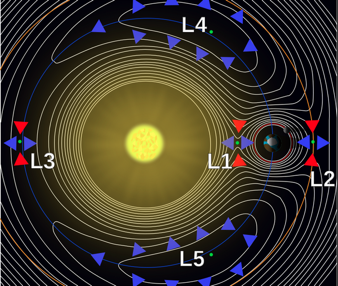
J.-L. Lagrange (1736-1813) demostró en 1772 que 3 cuerpos de masa arbitraria se pueden mover de manera que su disposición espacial permanezca inalterada (podríamos decir en equilibrio relativo). Hay dos situaciones geométricas que satisfacen esta condición: a) tres cuerpos dispuestos en línea recta en determinados puntos colineales; b) tres cuerpos situados en los vértices de un triángulo equilátero concreto. En la situación a) los puntos colineales se suelen designar como (L1, L2, L3) y en la b) los triangulares (L4 y L5). En general, estos se designan como puntos lagrangianos (aunque en realidad, de los cinco equilibrios relativos que se conocen, tres fueron encontrados por Lagrange y dos por Euler (1707-1783). En el caso del sistema Tierra-Luna más una sonda se suele hablar de los puntos de libración.
Si alguien siente la tentación de preguntar por el caso de 4 cuerpos, debe saber que por el momento no hay respuesta, pues no se ha encontrado solución. Y en el caso de mayor número de cuerpos la situación es bastante similar.
Construcción de los puntos de Lagrange
Supongamos que en el sistema Tierra-Luna, cuyas masas son M y m1, respectivamente, pretendemos situar una sonda espacial de masa m2 <<< m1 en el punto colineal L2. Ya que nuestra sonda está alineada con los dos cuerpos espaciales, habremos construido un sistema planetario con dos cuerpos girando alrededor de otro principal (el primario).
De las leyes de Kepler (1571-1630) sabemos que el periodo de revolución depende del radio de la órbita y que será mayor cuanto más lejano se encuentre del cuerpo masivo. Puesto que la masa m1 está situada en una posición orbital más próxima al cuerpo principal, recorrerá su órbita más velozmente que la sonda, rompiendo la alineación inicial de las tres masas.
Nos enfrentamos así de nuevo a un problema de tres cuerpos diferente del inicial. Pero dado que conocemos que cuando los tres cuerpos están alineados las atracciones entre M y m1 se suman, para la sonda de masa m2 esto es equivalente a sentir la atracción gravitacional de un único cuerpo celeste de masa, Mt, mayor que M (Mt = M + m1). Y puesto que debido a que el periodo de revolución es también inversamente proporcional a la masa del cuerpo principal, en el sistema de tres cuerpos alineados la sonda tenderá a recorrer su órbita más velozmente.
Alguien se puede preguntar si existe una distancia a la cual el periodo de revolución de la sonda sea igual al periodo de revolución de la masa m1.
Alguien se puede preguntar si existe una distancia a la cual el periodo de revolución de la sonda sea igual al periodo de revolución de la masa m1. Se trata así de sincronizar los dos movimientos orbitales para que tanto la sonda de masa m2 como el cuerpo de masa m1 giren en torno a M con la misma velocidad angular y por tanto permanezcan en la misma posición relativa manteniendo la alineación.
Lagrange demostró que esta distancia existe y es justo el punto de equilibrio colineal elegido (L2). Un razonamiento análogo se puede aplicar a los otros dos puntos colineales L1 y L3.
Para el caso de los puntos triangulares L4 y L5 el razonamiento es un poco diferente, pero también se basa en convertir el problema en uno de dos cuerpos.
En las proximidades del punto L1 de la órbita terrestre se encuentra orbitando el Solar and Heliospheric Observatory (SOHO, por sus siglas en inglés), destinado a estudiar el Sol. Desde 1996 se encuentra operativo y envía información sobre la estrella. Éste es un ejemplo de las misiones activas en la actualidad.
Griegos y Troyanos
Entre los asteroides hay dos familias que nos traen a la memoria los héroes de la Iliada de Homero. Estas agrupaciones no habitan, como acostumbran la mayoría de los asteroides, en el llamado Cinturón de Asteroides (entre la órbitas de Marte y Júpiter). De hecho, unos siguen a Júpiter y otros lo preceden, y se sitúan en los puntos triangulares lagrangianos de equilibrio L4 y L5.
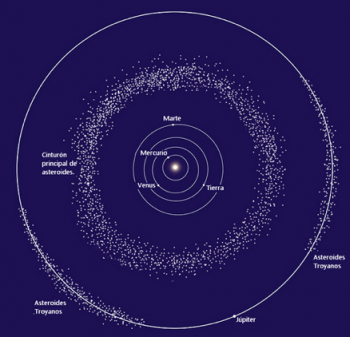
Los vencedores en la Iliada, los Griegos, preceden a Júpiter y los Troyanos lo siguen. Entre los Griegos se encuentran Aquiles, Menelao, Agamenón; en el segundo grupo hallamos a Eneas, Priamo y algunos más.

En general, los cuerpos celestes situados en alguno de los puntos triangulares lagrangianos se denominan “troyanos”.
Marte y Neptuno son planetas que orbitan el Sol acompañados de troyanos. En este par de planetas, se trata de pequeños objetos situados en el punto L4.
Un caso análogo se encuentra en la órbita de Tetis, satélite de Saturno. Esta luna está precedida del pequeño Calipso (60º grados antes en el punto L4) y es seguida por el pequeñito Telesto en el punto L5 (retrasado 60º).
La luna Dione (también de Saturno) viaja asimismo acompañada de dos pequeños troyanos, Polux que le sigue (60º por detrás) en el punto L5 y está precedido por Helena que ocupa el L4 (60º antes).
Estos datos y detalles concretos pueden indicar a quienes estén menos familiarizados con nuestro sistema planetario que las posiciones relativas de los distintos cuerpos que lo componen se explican con las leyes de la física que se cumplen en las cosas cotidianas en la Tierra. Además, como veremos en la segunda parte, podremos entender cómo podemos usar esto para la comunicación global. C2
Continuará…
Bibliografía
- HERRERA, R.M.: El piano y la Luna, Ciencia y Cultura C2, Monterrey, 2015
- HERRERA, R.M.: Resonancias en el Sistema Solar, Neomenia, Madrid, 2012
- HERRERA, R.M.: Rutas para viajar por el Sistema Solar, Ciencia y Cultura C2, Monterrey, 2015
- HERRERA, R.M.: Urania y los caminos del cielo, Ciencia y Cultura C2, Monterrey, 2015
- MILANI, A. & GRONCHI, C.: Theory of the orbit determination, Cambridge University Press, 2010
- MOSER, J.K.: Is the Solar System Stable?, The Mathematical Intelligencer. pp. 65-71 (1978)
- MOSER, J.K.: Stable and Random Motions in Dynamical Systems, Princenton Landarmarks in Mathematics
- POINCARÉ, H.: Les méthodes nouvelles de la mécanique céleste, Gauthier-Villars et fils, 1899 (reprint Dover 1957)
- SIEGEL, C.L. & MOSER, J.K. & KALME, Ch.I.: Lectures on Celestial Mechanics, Springer.
- SOHO https://www.nasa.gov/mission_pages/soho/index.html












