Este artículo se publicó originalmente en la Revista Avance y Perspectiva del CINVESTAV, Vol. 6 – Núm 4
La pandemia en la que el planeta entero ha estado inmerso durante 2020 nos ha cambiado la vida y ha demostrado que la lucha contra ésta es un fenómeno extremadamente complejo, que involucra no solo a la ciencia, la industria y la tecnología, sino además a la política, la economía, la cultura, la moral y la cooperación humana, que afectan en forma decisiva el desarrollo y la evolución de la enfermedad.
La pandemia ocasionada por el virus SARS-CoV-2 nos impacta al confrontarnos con una situación que pensamos superada hace tiempo: una enfermedad letal que se propaga con facilidad, para la cual no hay una cura específica ni una vacuna como medida preventiva. Al no haber antivirales que inhiban la proliferación del SARS-CoV-2, los médicos tratan a los pacientes atendiendo los síntomas que presentan, mejorando sobre la marcha los medicamentos adecuados para tal propósito y modificando los protocolos utilizados para atender en forma diferente los cuadros presentados por los enfermos.
Al no haber antivirales que inhiban la proliferación del SARS-CoV-2, los médicos tratan a los pacientes atendiendo los síntomas que presentan…
A falta de fármacos efectivos, los gobiernos implementaron diversas intervenciones no farmacológicas de carácter individual, tratando de evitar la saturación de los hospitales y por lo tanto muertes por falta de atención médica, tales como cuarentenas, distanciamiento de dos metros con otras personas, uso de mascarillas, lavado frecuente de manos y objetos de uso, etcétera. También han implementado otras medidas colectivas, como cierre de escuelas, cines, estadios, acceso restringido a parques, control de la cantidad de personas en el interior de supermercados, comercios y bancos. A medida que se verifica que las acciones no han sido lo suficientemente efectivas, nuevas estrategias se han intentado establecer en tiempo real en todo el mundo. Algunas de ellas incluso contrapuestas a las precedentes que se gestionan sobre un problema desconocido. Un año de pandemia nos demuestra que sin medidas farmacológicas es difícil alcanzar una inmunidad de rebaño que proteja a la población susceptible de contagio y que resulte en la desaparición de la enfermedad.
El esfuerzo de miles de científicos por combatir al SARS-CoV-2 ha obtenido resultados y se han logrado producir varias vacunas efectivas en un lapso de tiempo nunca visto antes. La pregunta obvia es si la vacunación masiva de la humanidad será suficiente para eliminar la pandemia, dada la rapidez con la que aparecen mutaciones más contagiosas del virus y la falta de medicamentos que curen la COVID-19. Ahora están empezando las campañas de vacunación de la población en algunos países del mundo, entre los cuales se encuentra México, y surgen varias preguntas inmediatas en torno a las estrategias adecuadas para la aplicación de las vacunas: ¿En qué orden deben repartirse éstas? ¿Cuántas personas hay que vacunar para lograr bajar el número de infectados y mitigar la pandemia? ¿A qué ritmo hay que vacunar para lograr dicho objetivo? ¿Cuál es la forma más eficiente?
¿Cuántas personas hay que vacunar para lograr bajar el número de infectados y mitigar la pandemia?
Para contestar estas preguntas hay que tomar en cuenta criterios de índole práctica, como por ejemplo la disponibilidad de las vacunas, la capacidad del sistema de salud para vacunar a determinado número de personas en un tiempo dado y cómo evitar la mayor cantidad de muertes posible. También hay que tomar en cuenta cuestiones morales, como por ejemplo, no discriminar a nadie al formular los programas de vacunación. En México ya se ha programado un orden de vacunación acorde con el riesgo de contraer la enfermedad y tratando de evitar los casos graves de la misma. A saber, se vacunará primero al personal de salud que está en contacto directo con los pacientes; en la segunda etapa se vacunará a las personas de 60 años o más y a personas con comorbilidades que agravan la enfermedad. En una tercera etapa se vacunará a personas entre 50 y 59 años, luego a las personas entre 40 y 49 años, y por último, al resto de la población. Los tiempos planeados implican terminar cada una de las etapas en aproximadamente un mes, con excepción de la última que durará aproximadamente 9 meses. En cuanto a las otras preguntas, un modelo matemático predictivo que simule diferentes escenarios puede ser muy útil para responderlas y guiar nuestras acciones.
Los autores de este trabajo elaboramos un modelo matemático [1,2,3] que simula la propagación de una pandemia no solamente en pequeñas áreas, sino también a través de un país en el que se dan brotes epidémicos en diferentes lugares de una manera no sincronizada. Además, toma en cuenta que la densidad de población no es homogénea y que las personas se mueven al azar tanto a cortas como a largas distancias. Decidimos utilizarlo para averiguar hasta qué punto será posible reducir el número de contagios si el programa anunciado por el gobierno de México se aplica de acuerdo a los planes ya descritos.
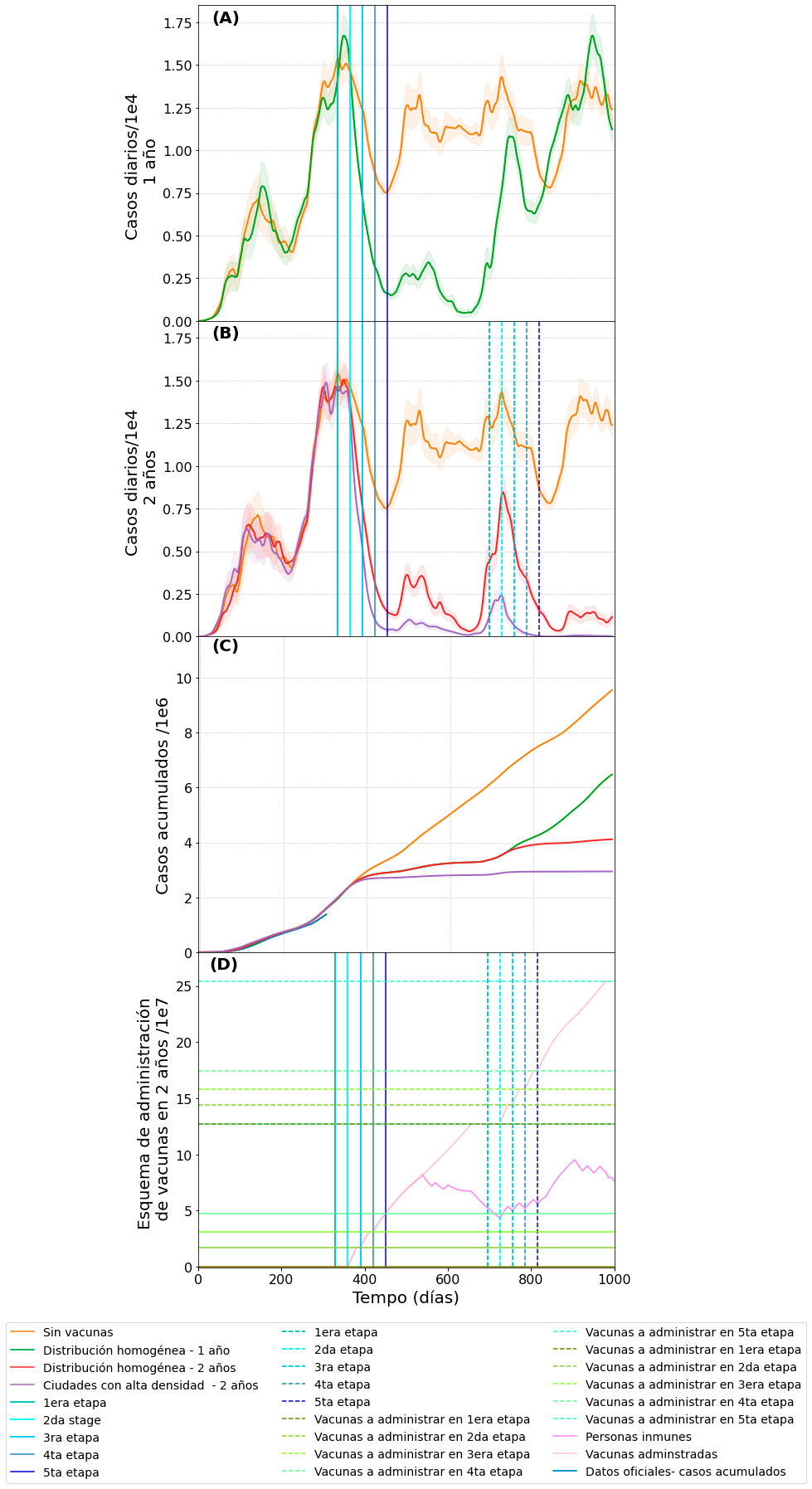
La Fig. (A) muestra los resultados al aplicar nuestro modelo matemático a la República Mexicana, en la cual mostramos la evolución de la pandemia predicha por los cálculos numéricos si la estrategia gubernamental se sigue durante un año (línea verde). La línea naranja representa el número de casos diarios suponiendo que no se administran vacunas. Todas las curvas temporales fueron obtenidas suponiendo que las restricciones a la movilidad se mantienen como hasta la fecha. Las líneas verticales indican los tiempos de administración de vacunas anunciados por el gobierno de México. Vemos una disminución inmediata de los casos, pero una vez pasado el tiempo de inmunidad que proporciona la vacuna y que para la figura estimamos en 180 días, la pandemia vuelve a surgir alcanzando los niveles que se tendrían sin vacunación.
La Fig. (B) muestra las predicciones del modelo si se administran vacunas siguiendo la misma estrategia por dos años (curva roja). Aquí agregamos la curva violeta que se obtendría si además se vacuna priorizando los lugares de mayor densidad de población, en los cuales, a través de la detección por pruebas PCR, se estaría vacunando a personas que pueden contagiar a más individuos, Lo que observamos es que la estrategia de poner un filtro de densidad de población al vacunar es bastante efectiva. Después del rebrote del segundo año la pandemia prácticamente desaparece. La Fig. (C) exhibe los mismos resultados en los casos acumulados. Obsérvese que la curva violeta es aproximadamente horizontal, lo cual significa el fin de la pandemia. La Fig. (D) muestra la cantidad de vacunas aplicadas en cada etapa de vacunación, dada la disponibilidad de las mismas.
La conclusión es clara: La pandemia no se puede derrotar simplemente vacunando discriminadamente, o imponiendo medidas de distanciamiento social, o haciendo pruebas PCR. El corolario es que se tienen que tomar en cuenta muchos factores y estudiar claramente la situación local de cada país, usando una combinación de estrategias que impidan en forma eficiente la propagación del virus. En particular, es muy importante hacer pruebas PCR al azar en regiones con alta densidad de población para aislar a los individuos que siendo asintomáticos esparcen la enfermedad sin saberlo. C2
Agradecemos el soporte financiero de la Universidad Nacional Autónoma de México (UNAM) y a la Alianza UCMX con la Universidad de California (UC), por el proyecto incluido en la convocatoria Special Call for Binational Collaborative Projects addressing COVID-19. RAB agradece la financiación de Conacyt a través del proyecto 283279.
Referencias
- (1) R.A Barrio, C. Varea, T. Govezensky, and M.V. José. Modeling the geographical spread of influenza a(h1n1): The case of Mexico. Applied Mathematical Sciences, 7(44):2143–2176, 2013.
- (2) Modelling Covid-19 epidemic in Mexico, Finland and IcelandRafael A. Barrio, Kimmo K. Kaski, Gudmundur G. Haraldsson, Thor Aspelund, Tzipe Govezensky. https://arxiv.org/abs/2007.10806
- (3) Detecting infected asymptomatic cases in a stochastic model for spread of Covid-19. The case of ArgentinaNadia L. Barreiro, Tzype Govezensky, Pablo G. Bolcatto, Rafael A. Barrio. http://arxiv.org/abs/2012.15209