Mire a su alrededor y elija cualquier fenómeno que le atraiga. Puede ser usted mismo, como sistema abierto compartiendo energía y materia con el medio ambiente, puede ser esa hermosa parvada que hace figuras impresionantes en el cielo o la tableta que usa para leer este artículo. Intente comprender el funcionamiento de cada fenómeno y se topará con la enorme diversidad de áreas que el ser humano ha creado para poder comprender el universo. Unos fenómenos requerirán áreas de mayor especialización otros solamente de experiencia, como la identificación de patrones de las estaciones de año que exitosamente descifraron nuestros antepasados y desarrollaron la agricultura, con las implicaciones que esto tuvo para la historia de la humanidad.
En el juego mundano que se propone en el párrafo anterior subyace el mecanismo que llevó al ser humano a existir como la especie dominante en la tierra, a pesar de ser el último en aparecer en la evolución. Ese acto de explicar lo que nuestros ojos ven, de entender la realidad que algunos le han dado por llamarlo ciencia, sentido común, etcétera, no es otra cosa que clasificar la aleatoriedad. Esto es, cuando se descubre el mecanismo de funcionamiento de un fenómeno, lo que ha hecho es encontrar que ese fenómeno no es aleatorio, que tiene una causa y usted la encontró. Todas las áreas de conocimiento científico, empírico, artístico, etcétera, son maneras de clasificar lo aleatorio. Por ejemplo, usted no estudió finanzas, más bien le enseñaron a abstraer los mercados financieros y representarlos en un “objeto” en forma de un arreglo de datos y ver qué tan aleatorio puede ser, y esto aplica para cualquier otra área de conocimiento.
En esta batalla del ser humano por clasificar la aleatoriedad surge la madre de todas las preguntas: ¿habrá fenómenos auténticamente aleatorios en el universo[1]? Dicho de otra manera, ¿habrá fenómenos a los que el ser humano sea incapaz de identificar una causa? Piense, por ejemplo, en la siguiente pregunta: ¿por qué todas la leyes que la especie humana ha descubierto no pueden explicar los primerísimos instantes del Big Bang? ¿Por qué tememos un horizonte de conocimiento? ¿Es que acaso somos nosotros el producto del único fenómeno genuinamente aleatorio del universo?
Intentando ser más explícito se propone el siguiente ejemplo. La evolución tuvo una dificultad muy grande para llegar a una vida tan compleja como la que vemos hoy en día, a partir de un ser tan extremadamente simple como el que se conoce como LUCA[2]. Por ejemplo [1], la célula humana tiene que fabricar proteínas; una proteína media (no muy chica, no muy grande) consta de unos 300 aminoácidos y tiene a su disposición 20 aminoácidos. Si la evolución se dio por mutaciones aleatorias, ¿cuántas combinaciones existen para hacer esa molécula en particular? La respuesta es 20300 (veinte elevado a la trescientos). Es muy improbable que la evolución hubiera tropezado con la combinación correcta mediante mutaciones aleatorias. Se tardaría millones de años, más años que el número de átomos que hay en el universo conocido. ¿Cómo le hizo la Evolución? ¿Qué sabe ella que nosotros no?
Cuando el ser humano se enfrenta con la dificultad de conocer el origen de un fenómeno, le asigna el carácter de aleatorio y asume una distribución uniforme para todas las posibilidades. Lo vemos en la teoría cinética de los gases en donde se admite que las propiedades físicas son iguales en cualquier dirección. Esto es, aún con falta de información el ser humano ha logrado satisfactoriamente proponer modelos matemáticos lo suficientemente buenos; a esto se le conoce como Simplicidad[3]. Sin embargo, este proceder falla en el ejemplo de la evolución. La naturaleza la encontró un atajo desconocido para nosotros.
Es claro, pues, que requerimos una herramienta para estimar mejor qué tan aleatorio es un objeto y, aunque ha habido muchos intentos para tratar de estimar la aleatoriedad, enseguida se expone una teoría novedosa que mejora cualquier paradigma existente, se llama Complejidad Algorítmica. La Complejidad Algorítmica se basa en la conexión que existe entre la Casualidad y la Computación. La conexión es lo que se le llama cálculo o computar, que se puede entender como un programa de computadora. El concepto de computar es, a grosso modo, la habilidad de guardar, transformar y trasmitir información. Piense en su celular, ¿qué hace el celular cuando usted envía un mensaje? ¿Cómo le hace su computadora para realizar el programa o código de la operación 2x +1? ¿Pero qué es la información?
Para entenderlo, tomemos un ejemplo. La información está relacionada con lo que nos hace ser nosotros y no otro individuo. Eso es esa diferencia genética de 1% entre el ADN de un chimpancé y el de un ser humano. Es esto lo que hace la diferencia y que además se puede medir usando las unidades de Bit (Binary Digit). Un Bit es la medida de la distinción entre dos posibilidades, 0 o 1, cierto o falso, sí o no, etcétera. A finales de los años 40 Claude Shannon propuso su Teoría de la Información, un formalismo construido axiomáticamente que mide la información en Bits, usando el concepto de entropía. Shannon tenía la encomienda de medir cuánta información se puede comunicar por un cable telefónico.
La pregunta surge: ¿es necesario un nuevo enfoque y por qué? Esto se contestará con esta interrogante retórica: ¿qué queremos? Lo que buscamos es tener una propiedad de un “objeto” que se pueda cuantificar claramente y que además mida qué tan aleatorio es el “objeto”. Pero queremos aún más, le exigiremos que sea más fundamental que la entropía de Shannon, que esta nueva propiedad no tenga la dificultad de lidiar con las distribuciones de probabilidad que en general se asumen uniformes. Esto es, que no se base en la aleatoriedad estadística porque eso oculta lo aleatorio subyacente en el objeto.
La teoría de la Complejidad Algorítmica[2] se basa en conceptos más fundamentales:
- Imprevisibilidad. La imposibilidad de predecir un resultado u objeto.
- Incompresibilidad. No se puede describir “algo” aleatorio de una manera simple o corta.
- Tipicidad. Un evento aleatorio no tiene algo particularmente especial.
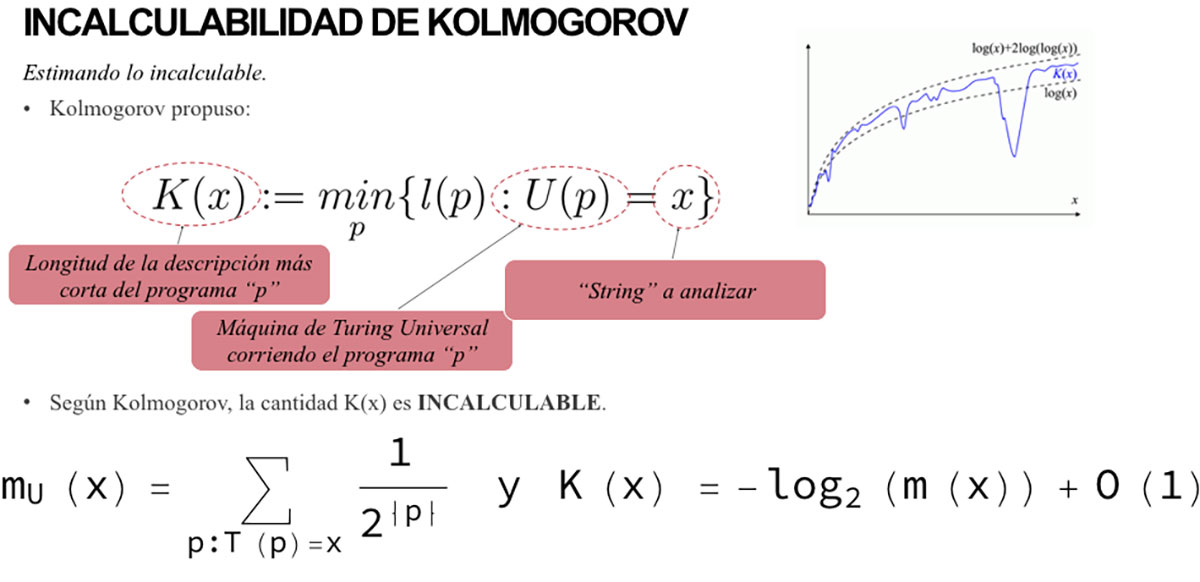
En el corazón de la teoría de la Complejidad Algorítmica está el concepto de la Máquina Universal de Turing. Tal vez hayan visto la película “El Código Enigma”. El personaje central es Alan Turing. La Máquina Universal de Turing es un objeto matemático que representa de manera abstracta una computadora. Uno alimenta a la Máquina Universal de Turing con un programa y la máquina lo realiza. Pero hay un problema, puede ser que el programa no termine nunca, lo que se llama el problema de parada. Para medir la Complejidad Algorítmica o la Complejidad de Kolmogorov, K, (ver Figura 1), se usan las mismas unidades de Bits como la Entropía de Shannon. Es la longitud en bits del código/programa más corto que corre en una Máquina Universal de Turing y que genera la secuencia a la que asociamos con “objeto”. A su vez ese “objeto” lo asociamos con un fenómeno. Pero K es incalculable, por el problema de parada mencionado.
Para lidiar con el problema de parada, el Dr. Héctor Zenil de la Universidad de Oxford, UK, es el pionero del Método del Teorema de Codificación [3]. En pocas palabras, esta teoría no calcula K directamente, es una aproximación usando la Probabilidad Algorítmica m. La Probabilidad Algorítmica nos dará la probabilidad de que un código/programa sea generado por muchos programas de computadora. Si un “objeto” es simple, tendrá muchos programas que lo generen, de lo contrario ese “objeto” será aleatorio, habrá pocos programas. K se relaciona con m como se muestra la figura 1.
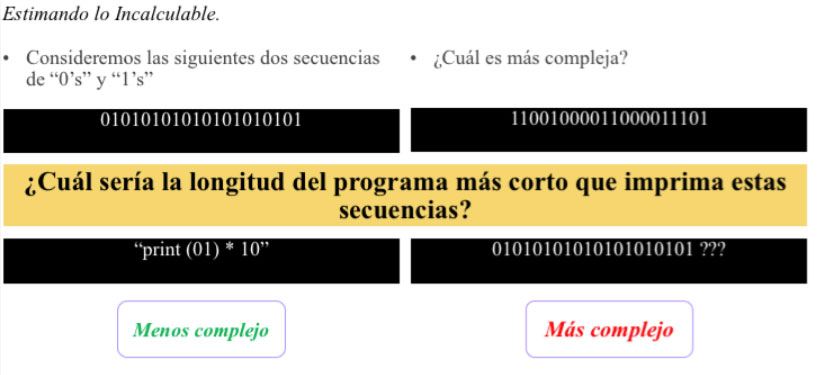
En la figura 2 hay un par de ejemplos: el ejemplo del lado izquierdo se puede simplificar con un código/programa corto, mucho más corto que la cadena y por lo tanto es simple. Por otro lado, en el de la derecha se requerirá un código/programa tan grande como la misma cadena que se quiere analizar. Ello indicaría que es más aleatorio, más complejo.
En resumen y regresando al inicio, esa sabiduría que tiene la evolución se ha estado probando con el nuevo paradigma que se acaba de presentar [4]. Después de todo, la evolución no es tan aleatoria; se ve sesgada por el entorno. Ese sesgo es asociado con una evolución algorítmica en el trabajo del Dr. Zenil et al., y ha dado buenos resultados en objetos pequeños, es decir, no tan grandes como sería una secuencia de ADN. Ciertamente aún falta mucho, este nuevo paradigma promete estimar mejor la aleatoriedad. Los problemas modernos requieren soluciones acordes. C2
Referencias
[1] https://www.quantamagazine.org/computer-science-and-biology-explore-algorithmic-evolution-20181129/.
[2] https://en.wikipedia.org/wiki/Algorithmic_complexity
[3] http://www.scholarpedia.org/article/Algorithmic_Information_Dynamics
[4] S. Hernández, H. Zenil and N. A. Kiani, Algorithmically probable mutation reproduce aspect of evolution such as convergence rate, genetic memory, modularity diversity explosions, and mass extinction, Royal Society Open Science, 5:180399, 2018.
[1] Asumimos como verdadero el Demonio de Laplace.
[2] Last Common Ancestor
[3] Puede consultar mi otro artículo llamado “La Complejidad: la siguiente gran revolución”.




María Guadalupe Olmos -
Buenas tardes, un artículo muy interesante.
Disculpe, se menciona, que en teoría, el único suceso que se considera aleatorio es lo que conocemos como el origen del universo, entonces, todos los demás sucesos no lo son?
Por otro lado, un suceso aleatorio también podría ser nombrado de esta forma por nuestra corta habilidad para lograr describirlo más ¨sintetizado¨?
Ya que a lo largo de la historia se a visto que sucesos que se consideraban aleatorios se les a podido encontrar un patrón, con forme las habilidades de análisis avanzan por así mencionarse.