La constante de Planck y el kilogramo

La balanza Kibble. Foto: Brian Resnick

14 de diciembre de 1900, seguramente un día frío en Berlín. Max Planck, un hombre de 41 años, serio y austero, dictaba una conferencia sobre la culminación frenética de varios años de su investigación sobre el problema de la “distribución del espectro normal de la radiación”. Quizá un extraño título para nosotros, pero no para sus escuchas de aquel día. Los asistentes a su seminario no comprendían del todo la teoría que Planck describía, pero permanecían muy atentos pues dicho trabajo satisfacía una máxima científica que calla al más escéptico: los resultados teóricos de Planck coincidían de manera casi perfecta con los datos experimentales. Lo que sí no sabían sus escuchas y, quizás ni el mismo Planck, es que estaban siendo testigos del nacimiento de una descripción de la naturaleza; revolucionaria, profunda, confusa, pero ante todo, extremadamente poderosa: la mecánica cuántica.

Como muchos lectores sabrán o habrán adivinado, el pasaje anterior pretende describir el día en el que Max Planck introdujo la constante h que lleva su nombre y que es la firma de la mecánica cuántica; es decir, si algún proceso o cantidad física tiene origen cuántico, involucra necesariamente a la constante h. Lo que no es muy conocido es que, en ese mismo trabajo, Planck también introdujo la constante de Boltzmann k y, con datos de su época, calculó el valor de la carga del electrón e y el número de Avogadro N_A. Lo curioso es que esas mismas cantidades, h, k, e y N_A, son los principales protagonistas del revolucionario cambio de unidades que el 20 de mayo de 2019 fue puesto en efecto por la Conferencia Internacional de Pesas y Medidas (CIPM), con sede en París. Dicho cambio redefinió el kilogramo, el kelvin, el ampere y el mol, que son las unidades de masa, temperatura, corriente y cantidad de materia, respectivamente. Es un cambio debido al increíble avance científico y tecnológico de los últimos 100 años. Y fue el trabajo de Planck el que marca el inicio de la gran transformación.

A mediados del siglo XIX, los nubarrones del cambio en la concepción del mundo aparecían de forma dispersa en variados ámbitos científicos. Por un lado, se descubría que los cuerpos calientes no sólo emitían luz, sino que también la absorbían y, más interesante, lo hacían en las mismas frecuencias o longitudes de onda de la luz; es decir, si un material absorbía en una frecuencia dada, emitía también en la misma. Se entendía a su vez que la distribución o cantidad de la luz emitida por cualquier cuerpo, dividida por la cantidad absorbida, era la misma para todos los materiales y que sólo dependía de la frecuencia de la luz y de la temperatura del cuerpo, sin importar de que estuviese hecho. Esa era la “distribución del espectro normal de la radiación” aludida arriba. El problema fue detallado por Gustav Kirchhoff en la década de 1850 y se pensaba que no debería de ser complicado de resolver, dado su carácter “universal”. ¡Poco sabían! Este acertijo lleva también el nombre del “problema del cuerpo negro”, pero ese es un detalle técnico que dejaremos de lado. De manera paralela, en esos mismos años, y en parte como consecuencia de la revolución industrial, el gran Rudolf Clausius le daba los puntos finales a su monumental obra que ahora llamamos Termodinámica y que describe las transformaciones de trabajo en calor y viceversa en todos los procesos naturales y los desarrollados por los humanos, como son todas las máquinas en nuestro entorno. La Termodinámica está esencialmente contenida en dos leyes: la Primera, que nos dice que la energía sólo se transforma, que no se crea ni se destruye, y la Segunda, que enuncia que la irreversibilidad es parte de nuestra realidad. La segunda ley se manifiesta a través de una cantidad que hasta el día de hoy, sigue sonando exótica: la entropía. La ley dice que, en cualquier proceso que ocurra en un cuerpo aislado, la entropía nunca disminuye. O aumenta o se queda igual.

El tercer ingrediente en la historia es que la idea de que todos los cuerpos o materiales están hechos de átomos y moléculas cobraba cada vez más fuerza, aunque había un sinnúmero de detractores por la falta de evidencia experimental. Un personaje central en este desarrollo fue el físico austriaco Ludwig Boltzmann que, apenas unos diez años después del trabajo de Clausius, le asestó un golpe devastador al aseverar que la irreversibilidad es probabilística, es decir que no es una ley “exacta” de la naturaleza. Boltzmann alegó que el movimiento de los átomos, al seguir las leyes reversibles de la mecánica clásica, implicaban que la irreversibilidad realmente no puede existir. Enfatizaba que la aparente irreversibilidad es una consecuencia del número inimaginable de átomos que tienen los cuerpos macroscópicos. Así, un proceso aparece como irreversible realmente por ser lo más probable en ocurrir, pero lo contrario estrictamente no es imposible. Las ideas de Boltzmann, sin embargo, no sólo eran enunciados filosóficos, sino que estaban substanciadas por una teoría matemática que daba lugar a una fórmula de la entropía en términos de una cantidad probabilística, que la relaciona con el mundo atómico. Esta fórmula es uno de los pilares de la física moderna y regresaremos a ella más adelante.

Max Planck, que había estudiado la Termodinámica con sus mismísimos creadores, hallaba absurdas y casi repugnantes las ideas de Boltzmann y del atomismo en general. Las leyes de la Termodinámica eran eso, “leyes”, y no el producto del supuesto azar microscópico. Cabe enfatizar que Planck no estaba solo en su actitud escéptica y antagónica hacia Boltzmann y, de hecho, aunque quizás es un mito, se dice que el final trágico de la vida de Boltzmann se debió a ese constante enfrentamiento que sostuvo por muchos años con sus acérrimos críticos. Planck, caracterizado por una gran seriedad y determinación en todo lo que hizo en su vida, decidió en 1890, al ser nombrado profesor de la Universidad de Berlín, que dedicaría sus esfuerzos científicos a demostrar que la Segunda Ley de la Termodinámica era realmente una ley y que usaría el problema de la radiación de Kirchhoff como su caballito de batalla. Un detalle técnico, pero muy importante, es que dado que los cuerpos en equilibrio térmico emiten la radiación que Planck deseaba describir. En vez de estudiar a la radiación electromagnética misma, produjo un modelo de un cuerpo que, hipotéticamente, estaría compuesto por “resortitos” con carga eléctrica que pudieran emitir y absorber la mencionada radiación. De esta manera, transformó un complejo problema de radiación, que no sabía como formular, a uno de un conjunto de osciladores (nombre científico de los resortitos) en equilibrio térmico, sistema con el que Planck se sentía más cómodo. Planck halló que la fórmula de la “distribución normal de la radiación” podía calcularse si resolvía el problema termodinámico de los osciladores, es decir, si calculaba la entropía de dichos osciladores.

La historia completa es larga y compleja, baste decir aquí que Planck llegó al modelo arriba mencionado en 1893.

Después pasaron seis largos años en los que hizo toda clase de intentos sin gran éxito, pero en los que poco a poco fue cediendo de manera renuente a las ideas “heréticas” de Boltzmann. Y es aquí donde entran los experimentos que sus colegas, Ferdinand Kurlbaum, Otto Lummer, Werner Pringsheim, Heinrich Rubens y Wilhelm Wien, hacían en Berlín por esa época, midiendo la distribución normal de la radiación. Incidentalmente, había fondos para realizar esos experimentos pues Alemania estaba decidida a electrificar sus ciudades y a iluminarlas con focos, o bombillas, de filamento metálico, como los que ya casi no se usan. El desarrollo de esos focos necesitaba de conocer la radiación que emitían esos filamentos. En 1897 se tenía un gran avance experimental debido a Wien principalmente, y Planck postuló una fórmula de la entropía de sus osciladores que parecía explicar la distribución de la radiación que medían sus colegas. El problema fundamental al que se enfrentaba Planck es que él mismo no sabía cómo calcular o justificar esa fórmula de la entropía. Pero no se arredró, creía que tarde o temprano se le ocurriría cómo hacer el cálculo. No parecía tener prisa. Hasta que llegó el famoso domingo 7 de octubre de 1900. Ese día, durante una comida, su colega Heinrich Rubens le confirmó algo que ya se veía venir: los nuevos experimentos demostraban que la fórmula que creían describía a la distribución, era incorrecta. Planck no se asustó, se sentó a trabajar, y usando sus artes termodinámicas, postuló de manera empírica, es decir, sin tener un sólido fundamento, una fórmula nueva de la entropía que podría ser mejor que la anterior. Se la envió a Rubens y, éste, en unos cuantos días le contestó algo que dejo perplejo a Planck: su nueva fórmula era perfecta, en el sentido que describía todos los experimentos que se tenían. Planck ahora sí se puso tenso pues bien sabía que su fórmula, aunque correcta, no tenía ningún fundamento. Inició lo que años más tarde llamaría el trabajo más extenuante que había hecho en su vida. Fueron sólo dos meses, pero increíblemente intensos. Seguro dormía muy poco. El problema era que no sabía cómo calcular esa entropía de los osciladores. Y en un arranque de desesperación, pero también de mucho valor personal y sobre todo científico, decidió recurrir a la dichosa y “desprestigiada” fórmula de la entropía de Boltzmann, en la que no creía inicialmente. Aceptarla era equivalente a abrazar con todo fervor la hipótesis de que todo en la naturaleza está hecho de átomos y moléculas. Planck estudió los trabajos de Boltzmann y se topó con un problema que ni él ni nadie se había topado antes y que, ni más ni menos, abría la caja de Pandora de la mecánica cuántica: el problema estribaba en que para poder aplicar la fórmula de Boltzmann, y que ésta a su vez coincidiera con los resultados experimentales, se veía forzado a suponer que la energía de los osciladores, al oscilar, valga la redundancia, no podía tomar cualquier valor. No, la energía de un oscilador sólo podía tomar valores enteros de una cantidad básica de energía –que ahora llamamos cuantos de energía–. Es decir, la energía de los osciladores sólo podían ser 1 o 2 o 3, etcétera, veces la energía básica. Para la comprensión de la física de la época eso era completamente absurdo. Es como si dijéramos que nuestro peso corporal sólo puede valer números exactos de kilogramos, es decir, que sólo pudiéramos pesar 60 kilogramos, 61, o 62, pero que fuera imposible pesar 60 kilos y 350 gramos, por ejemplo. ¡Suena absurdo! Pero de nuevo, caracterizado por ese valor que no le temía a la crítica, y dado que si no hacía esa suposición los experimentos no se explicaban, Planck se aferró a ese “absurdo” y así lo expuso aquel 14 de diciembre de 1900. Un poquito más técnico, Planck halló que esa cantidad básica, o cuanto de energía de los osciladores, era proporcional a una constante que bautizó como h y cuyo valor extrajo de los datos experimentales. Aunque recibió críticas de nuevo, no se preocupó demasiado pues creía que lo podría explicar con el tiempo. Poco sabía Planck que esa constante no tiene explicación al día de hoy. Es lo que llamamos, una “constante fundamental”, eufemismo científico para decir que es una “ley de la naturaleza” que no podemos entender ni explicar. Así es y punto. Es como pretender explicar por qué el Sol y la Tierra se atraen. No sabemos, se atraen y no hay explicación. A eso le llamamos la Ley de la Gravitación Universal de Newton y no la explicamos, la entendemos y la aplicamos… Luego, en 1905 Albert Einstein usó esa constante para explicar el efecto fotoeléctrico y en 1906 para entender unas rarezas del diamante; después, en 1913 Neils Bohr la usó para desarrollar su modelo del átomo, que a su vez explicaba otros experimentos, y el resto es historia. Ahora tenemos electrónica, computadoras, láseres, comunicaciones satelitales. Sabemos que sí estamos hechos de átomos, no sólo nosotros sino las estrellas también, entendemos que la genética está contenida en la molécula de DNA y la lista es interminable. Vivimos una revolución tecnológica que afecta la vida comercial, social, industrial y científica. Todo es consecuencia del valor de Planck de aferrarse a esa constante h.

Es lo que llamamos una “constante fundamental”, eufemismo científico para decir que es una “ley de la naturaleza”, que no podemos entender ni explicar. Así es y punto.

En la fórmula final de la “distribución normal de espectro de energía de la radiación”, ahora llamada “distribución de Planck”, no sólo aparece la constante h, Planck también introdujo otra constante relacionada a la temperatura de la radiación, a la que llamó k. Esa constante, debido a que es parte de la afamada fórmula de Boltzmann, se le llama “constante de Boltzmann”. Pero Planck no se detuvo ahí, se dio cuenta que con la constante k y otra cantidad empírica del siglo XIX, llamada la Constante Universal de los Gases, se podía calcular el número de Avogadro N_A, que es el número con el cual sabemos cuántos átomos hay un cantidad dada de cualquier sustancia. Y más, había otra cantidad llamada la Constante de Faraday que depende de N_A y de la carga del electrón e, con la cual calculó el valor de la última. Aunque no es esencial para el hilo de esta narración, escribimos los valores que halló Planck[1]:

h = 6.55 X 10^-34 joules-seg

k = 1.346 X 10^-23 joules/grado K

N_A = 6.175 X 10²³

e = 1.56 X 10^-19 coulombs

Como veremos más abajo, estos números son muy cercanos a los exactos del 20 de mayo de este año. Son resultado de la finura de los experimentos de los colegas de Planck y atestiguan lo precisa y perfecta que es la fórmula final de Planck. Ahora sabemos que lo es porque es una “formula cuántica” y ahora sabemos o aceptamos que el universo es cuántico.

¿Y cómo está relacionado el kilogramo con la constante de Planck?

La respuesta es un poco complicada, pues no existe una relación directa entre los anteriores, pero sí en la forma en que ahora mediremos la masa. Hablemos entonces no sólo del kilogramo sino también de las demás unidades del Sistema Internacional de Unidades, abreviado SI. Primero debemos entender que las unidades de medida son arbitrarias. Son el invento de algunos personajes en algún momento histórico, nacidas de la necesidad de poner un poco de orden en nuestras relaciones comerciales, industriales, sociales y científicas. Sería muy caótico vivir sin patrones de medida. Es claro que podemos medir las distancias entre dos lugares o el tamaño de algún objeto con metros, centímetros, yardas, pies, o con cualquier escala que se nos antoje. Lo mismo ocurre con el tiempo, cualquier movimiento de un sistema físico que se repita se puede usar como reloj. Cuenta la leyenda que Galileo medía el tiempo con su propio pulso. Y, de la misma manera, el peso o masa de los objetos puede medirse con kilogramos, onzas o comparándolos en una balanza con otro objeto arbitrario de referencia. Sin embargo, esto no es útil y sí causa muchas dificultades, por lo que los humanos creamos referencias o patrones que sirven para todos y nos permiten comunicarnos para realizar todo tipo de transacciones de manera clara y ordenada. Así, aunque desde Copérnico y Newton se necesitaba de una medida precisa de las distancias, no fue sino hasta después de la Revolución Francesa en 1789 que se decidió por el “metro” que, originalmente, era tal que cualquier circunferencia de la Tierra que pasara por los polos, midiera “exactamente” 40 millones de metros, o 40 mil kilómetros. La medida del tiempo se pierde en la historia y ya los egipcios y los babilonios tenían al movimiento de la Tierra como la referencia, tal que el día tiene 24 horas, las horas 60 minutos y los minutos 60 segundos. Y el kilogramo no es la excepción. En el París de finales de los 1700, la corte de Luis XVI decidió que era momento de poner orden en el desastre de las medidas de masa que daban lugar a muchos fraudes. Se decidió que el kilogramo era lo que pesaba un litro de agua. Hasta la fecha ésta es una de las maneras más sencillas de “sentir” qué es un kilogramo. Estas definiciones no han impedido que otras se mantengan hasta el día de hoy, como el sistema inglés con libras y onzas para el peso y el pie y las pulgadas para las distancias. Para el tiempo, todos usamos los segundos, afortunadamente. El problema con las anteriores definiciones del segundo, metro y kilogramo es que no son precisas. Los avances científicos y tecnológicos, así como las necesidades comerciales e industriales, generaron de forma implacable la necesidad de patrones más precisos y, de preferencia, que no dependieran de artefactos hechos por nosotros mismos. Aunque hablaremos esencialmente del kilogramo, por su novedad, cabe resaltar que el segundo y el metro fueron redefinidos. El primero en 1967, con la frecuencia de transición atómica de un estado del cesio 133 (suena muy complicado, lo es) y el metro, en 1983, usando el hecho de que la velocidad de la luz es una “constante fundamental” de la naturaleza. Sugerimos al lector consultar Wikipedia para una rápida y adecuada explicación de dichas definiciones. Veamos lo que pasó con el kilogramo.

Debemos entender que las unidades de medida son arbitrarias. Son el invento de algunos personajes en algún momento histórico, nacidas de la necesidad de poner un poco de orden en nuestras relaciones comerciales, industriales, sociales y científicas.

Muy pronto, después de la definición del kilogramo como el peso de un litro de agua, se descubrió que era muy poco práctica y susceptible de muchos errores. En su lugar se decidió usar una barra de metal que pesara lo mismo que dicho litro de agua, bien medido. El 20 de mayo, pero de 1875, se decidió por un pequeño cilindro de 90% de platino y 10% de iridio que, hasta el día de hoy, se encuentra celosamente guardado en un sótano a las afueras de París. Ese pequeño cilindro era “el kilo” y nada más. Por supuesto, se hicieron copias del cilindro, lo más fielmente posibles, y se llevaron a otros países donde, a su vez, se usaban para calibrar todo tipo de balanzas. Increíble, pero desde 1875 hasta 2019, ese fue nuestro patrón de peso. Y sucedió lo que era de esperarse. Con los años, las réplicas del kilogramo de París empezaron a diferir entre ellas, por muy poquito, por millonésimas de kilogramo, pero era evidente que no pesaban lo mismo. Y dado que la tecnología moderna requiere de cada vez mayor precisión había llegado la hora de hacer algo radical y “redefinir” el kilogramo, usando de nuevo nuestro conocimiento del universo, tal que “cualquiera” de nosotros pudiera medir la masa o el peso sin necesidad de un patrón en algún otro lugar del planeta.

El 20 de mayo, pero de 1875, se decidió por un pequeño cilindro de 90% de platino y 10% de iridio que, hasta el día de hoy, se encuentra celosamente guardado en un sótano a las afueras de París.

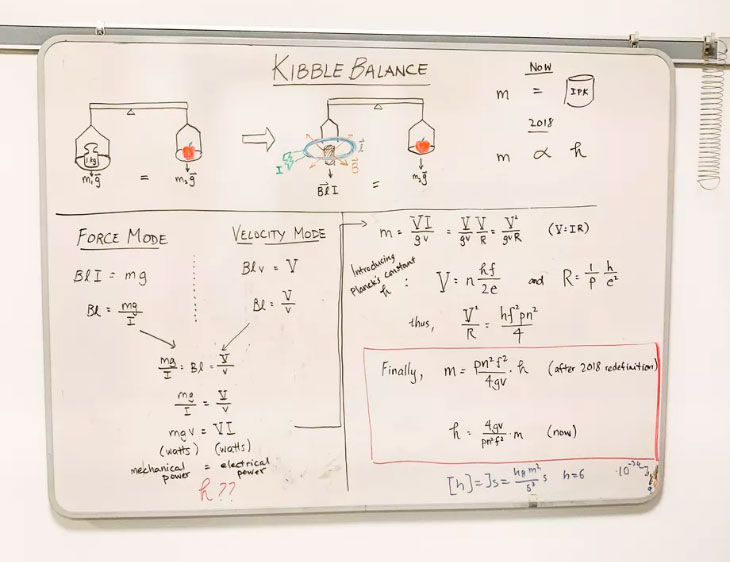
Se decidió entonces medir el peso de los objetos con un balanza mecánica y electrónica que usara cantidades fundamentales fijadas por la mecánica cuántica, como la constante de Planck h. Dicha balanza fue concebida en 1976 por Brian Kibble y, en su honor, se llama “balanza de Kibble”. Veamos como funciona. Pesar es comparar la fuerza que necesitamos hacer para equilibrar un peso dado en una balanza. Si conocemos dicha fuerza necesaria, entonces sabemos el peso del objeto. Y si conocemos la aceleración de la gravedad en el lugar donde se encuentra la balanza, entonces podemos saber la masa del objeto. Ingenioso, ya no necesitamos un patrón de medida, lo que necesitamos es poder medir la fuerza necesaria para equilibrar la balanza. Pensemos entonces en una balanza en la que en un lado se tiene un platillo donde se coloca el objeto a medir. En el otro lado del brazo de la balanza colocamos una bobina eléctrica, que se encuentra expuesta al campo magnético de un imán muy potente. Hacemos entonces pasar una corriente eléctrica por la bobina y, se sabe desde el siglo XIX, que la bobina con corriente siente una fuerza debida al campo magnético del imán. Es decir, podemos lograr, que al pasarle corriente a la bobina, el imán la “jale” en sentido contrario al peso del objeto en el otro brazo de la palanca. La balanza se equilibrará cuando la corriente que pasemos sea la apropiada para compensar el peso del objeto. El primer reto es medir esa corriente eléctrica. Y aquí entra la mecánica cuántica por medio de los llamados “efecto Josephson” y “efecto Hall cuántico”.

La “balanza de Kibble”, concebida en 1976 por Brian Kibble . Jennifer Lauren Lee, del U.S. National Institute of Standards and Technology (NIST)

El efecto Josephson, descubierto por Brian David Josephson en 1962 y por el cual recibió el premio Nobel de física en 1973, nos permite medir voltajes de manera muy precisa. El voltaje obtenido depende de la constante de Planck (y de la carga del electrón). El efecto Hall cuántico, descubierto por Klaus von Klitzing en 1980 y, también, por el cual se le otorgó el premio Nobel de física en 1985, nos permite medir la resistencia de un material ad-hoc, de nuevo en términos de la constante de Planck. Combinando estos dos efectos, se puede medir la corriente de la balanza. El problema es que para medir la fuerza del imán no es suficiente con saber la corriente. Existe un factor adicional muy complicado de medir. Aquí entró el ingenio de Kibble. Se dio cuenta de que si apagamos la corriente, entonces la fuerza del imán ya no la siente la bobina y la balanza empieza a moverse por estar desbalanceada. Sin embargo, al moverse la bobina sin corriente, se genera un voltaje en la bobina, descubrimiento que hizo Joseph Faraday en 1831 y que es la base de todos los motores y generadores eléctricos. Kibble halló que si medía dicho voltaje y la velocidad con la que la bobina se mueve, entonces aquel factor adicional que se necesitaba para medir la fuerza del imán ya no era necesario. El voltaje se mide de nuevo con el efecto Josephson y, otra vez, entra la constante de Planck en juego. Así, se llega a una fórmula que expresa a la masa del cuerpo en cuestión, en términos de cantidades que pueden medirse de manera muy precisa e, importantísimo, de forma proporcional a la constante de Planck.

Al principio, el uso de la balanza de Kibble era al revés: se usaba la masa del cuerpo, pesada con alguna copia del kilo de París y, con las mediciones posibles, se determinaba el valor de la constante de Planck cada vez con más precisión. Sin embargo, llegó el momento en que se obtuvo un “empate”: el error inherente en las copias del kilogramo de París era igual o peor que el error en las mediciones de la constante de Planck. Era hora de voltear el procedimiento. Se hicieron experimentos en varios lugares del mundo donde tenían balanzas de Kibble (aunados a otras técnicas menos fáciles) y se compararon los valores de la constante de Planck. Se halló que las primeras 9 cifras significativas del valor de h eran las mismas. Y entonces se hizo el cambio radical. Por acuerdo de todos los países del CIPM se decidió por un valor fijo y constante de h que tiene las siguientes cifras:

h = 6.626070150 X 10^-34 joules-seg

Con este valor, y usando la balanza de Kibble, desaparece la necesidad del patrón de masa. Es decir, la masa del objeto en la balanza está determinado por las mediciones de corriente, voltaje, velocidad y gravedad del aparato, y por el valor fijo de h. El kilogramo de Paris ya no es la referencia. De hecho, su peso ya no es de 1 kilogramo. Es unas millonésimas más de lo que “era” y con los años, su peso irá cambiando, como todo en la naturaleza, incluidos nosotros. A veces subirá, a veces bajará, dependiendo de las condiciones de humedad, del aire a su alrededor, del hecho que los átomos del cilindro a veces se escapan del mismo, etcétera.

Así es como funciona la balanza Kibble. Foto; Brian Resnick

¿Por qué decimos que el cambio de unidades es “radical”? Elaboremos un poquito. Recordemos que las unidades de medición son arbitrarias, aunque una vez que están definidas, tenemos un compromiso de respetarlas. Y eso hacen todos los países del mundo. Es una convención, decimos los científicos. Las unidades que tenemos, metro, segundo, kilogramo (y ampere, kelvin, mol y candela) son, como ya dijimos, un capricho de algunos humanos en algún momento histórico. Entonces ocurre que, en esas unidades, las constantes fundamentales de la naturaleza, como la velocidad de la luz, la constante de Planck y la carga del electrón, tienen valores muy “raros” e “inexactos”, como el que apuntamos arriba de h, en vez de que tuvieran valores más sencillos y fijos o constantes, por ser fundamentales. Es decir, su valor debe ser fijo y constante, o al menos la ciencia del día de hoy así nos los indica. ¿No sería más fácil que la constante de Planck valiera 6 y la velocidad de la luz 3, por ejemplo? Sí. El mundo científico estaría feliz, pues nuestros cálculos serían más fáciles. Lo malo es que “desaparecerían” el metro, el kilogramo y el segundo; en otras palabras, ya no tendrían sentido si a h le diéramos otro valor. Esto no lo podemos hacer, salvo crear un caos a nivel mundial pues tendríamos que cambiar todas nuestras mediciones, transacciones, etc. No debemos hacerlo y lo mejor es quedarnos con el “metro”, “segundo” y “kilogramo”, aunque estrictamente los “nuevos” tendrán un valor ligeramente diferente. En otras palabras, hacer que h tenga ese valor fijo, o que la velocidad de la luz sea exactamente 299792458 metros por segundo, es completamente equivalente a darles cualquier otro valor fijo, como 6 o 3. Nos quedamos al mismo tiempo con la arbitrariedad de nuestros antepasados y con un nuevo sistema de unidades, universal y fundamental, y que no debería de cambiar más … Ya lo veremos.

Para concluir, regresemos a los valores que Planck halló en 1900 para h, k, N_A y e. Con procedimientos experimentales similares a los de la balanza de Kibble, el 20 de mayo de 2019 se fijaron los siguientes valores de forma exacta.

h = 6.626070150 X 10^-34 joules-seg

k = 1.380649 X 10^-23 joules/grado K

N_A = 6.02214076 X 10²³

e = 1.602176634 X 10^-19 coulombs

Si los comparamos con los originales de Max Planck escritos arriba, la diferencia es aproximadamente del 1%. ¡Muy bien!, dado lo rudimentario de los experimentos de la época. En poco más de 100 años, todo nuestro gran avance científico y tecnológico se reflejan fríamente en esas largas cifras, fijas y exactas.

[1] El lector experto perdonará al autor la libertad de traducir los cálculos de Planck del sistema de unidades cgs, que él usaba, al SI. C²

Sobre el autor

Victor Romero Rochin

Miembro del Sistema Nacional de Investigadores, nivel 3. Investigador titular en Instituto de Física, UNAM

Sus intereses científico/académicos son: gases atómicos ultra fríos; termodinámica, turbulencia. Le gusta dar clases; ha llevado a México a los primeros lugares en Iberoamérica en la Olimpiada de Física.