La informática tiene nombre de mujer

Ciencia

La informática tiene nombre de mujer

23 febrero, 2017
|
POR Francesca Camilli, Donatella Merlini, Maria Celia Verri y Gianna Reginato
|
0 COMENTARIOS
|
Like 0
|
779

En sus notas Ada observa que “la máquina es capaz, en ciertas circunstancias, de descubrir cuál entre dos o más contingencias posibles se ha verificado y modificar el comportamiento futuro de acuerdo a tal caso”, y añade más adelante, “las tarjetas de las operaciones pueden leerse secuencialmente, pero también en sentido opuesto para poder repetir así el proceso […] es posible realizar ciclos dentro de ciclos”. Si comparamos estas afirmaciones con el teorema de Böhm-Jacopini de 1966: “Cada algoritmo puede ser implementado sólo con tres estructuras de control: secuencia, selección y ciclo”, podemos apreciar la clarividencia del pensamiento de Ada Lovelace, que había individualizado las tres estructuras de control fundamentales en la máquina de Babbage. A esto se pueden añadir otras tres citas de su trabajo también ellas extraordinariamente visionarias:

El complejo control de la Máquina Analítica se produce sobre la manipulación ejecutiva de símbolos numéricos y algebraicos que permite su uso para el cálculo simbólico, no sólo numérico.
El mecanismo de las operaciones se pueden poner en práctica para cualquier objeto sobre el cual se puede operar; puede actuar sobre cualquier objeto, a condición de que estos objetos sean susceptibles de relaciones mutuas fundamentales expresadas en la ciencia abstracta de las operaciones […] supongamos que las relaciones fundamentales de una nota en la ciencia de la armonía y de la composición musical fuese susceptible de tal expresión de adaptación, la Máquina podría componer pistas de música de cualquier complejidad y duración:
No es preciso alimentar ideas exageradas sobre los poderes de la Máquina Analítica. La Máquina Analítica no tiene ninguna pretensión de originar cualquier cosa. Sólo puede efectuar lo que nosotros le indicamos que haga. Puede realizar análisis, pero no tiene el poder de anticipar alguna relación o verdad analítica.

Ada_Lovelace_01 — Ada porron condesa de Lovelace

De estas citas se evidencia cómo Ada estaba en condiciones de ver la potencialidad presente en la Máquina Analítica, de prever sus futuras aplicaciones y de definir, al mismo tiempo, también sus límites. Incluso si las ideas proviniesen de Babbage – como alguno de sus biógrafos sostienen- Ada ha sido en cualquier caso capaz de ilustrar al mundo el funcionamiento de la Máquina Analítica y con sus elementos fundamentales. Si Babbage fue el padre de la Máquina Analítica, Ada intuyó su potencia e inventó el lenguaje, convirtiéndose así, a todos los efectos, en la madre.

La salud de Ada comenzó a empeorar: el uso de drogas para aliviar los dolores influyó sobre su carácter. Las relaciones con su marido comenzaron a enfriarse e incluso los hijos fueron dejados al cuidado de la abuela. Dedicándose a los juegos de azar Ada dilapidó sus joyas, los únicos bienes de los cuales podía disponer personalmente; tuvo probablemente relaciones extraconyugales y a los 37 años, el 17 de noviembre de 1852 falleció por un tumor del útero.

La hechicera de los números

Las notas más profundas que Ada añadió a la traducción del artículo de Menabrea dieron lugar, como ya dijimos, a un trabajo conspicuo tres veces más largo que el artículo original. Ada firmó el trabajo con sus iniciales A. A. L. porque hacer público su nombre no se correspondía con su rango. En la nota que la hizo famosa Ada desarrolló un procedimiento de cálculo de los números de Bernoulli, muy adecuado para la Máquina Analítica. Se trataba de un ejemplo mucho más complejo del desarrollado por Menabrea para describir el funcionamiento de la máquina. No es fácil determinar la contribución original de Ada. La biografía de Moore (1977) y Stein (1987) sembraron dudas sobre la capacidad real de Ada, mientras que las de Toole (1992) y Baum (1986) demuestran lo contrario. El primer argumento de la discusión es la preparación matemática real de Ada que es difícil de comprobar. El único testimonio, por otra parte, es el conjunto de las numerosas cartas que Ada había intercambiado con sus maestros, pero muchas de ellas se han perdido. En particular resulta imposible encontrar el volumen de apuntes que Ada usaba durante su estudio con el famoso matemático Augustus de Morgan. Las alabanzas que De Morgan y Babbage realizaron a Ada sobre su competencia matemática pueden haber sido dictadas por el deseo de contrarrestar un ambiente intelectual en el que las mujeres eran casi totalmente ausentes y la mayoría de la hombres no eran especialmente brillantes.

La diferencia de rango podría contaminar el juicio sobre Ada.

También la diferencia de rango podría contaminar el juicio sobre Ada. Además, el estudio por correspondencia con De Morgan era irregular y discontinuo y no documentado por exámenes reales. El biógrafo Woolley sostiene que Ada consideraba las expresiones algebraicas como espíritus y hadas y permanecía dudosa frente a la manera en que una fórmula podría ser derivada de otra.

Sin embargo, es indiscutible la originalidad de su pensamiento puesto que Ada no se contentaba con aprender reglas y procedimientos, sino que quería entender la razón de todo. En cuanto a la polémica sobre la autoría del programa para los números de Bernoulli, lo cierto es que se trata de un proyecto de gran envergadura y original, que probablemente Ada y Babbage realizaron en colaboración. Ciertamente Ada tenía perfectamente claro tanto el algoritmo de cálculo como el correspondiente programa para la Máquina Analítica.

Una secuencia infinita

Para entender el contenido de la Nota G es necesario saber qué son los números de Bernoulli. Estos números fueron encontrados por el matemático suizo Jacob Bernoulli (1654-1705) en relación con la suma de potencias de enteros sucesivos y se puede encontrar en su obra Ars Conjectandi, publicada póstumamente en 1713. Se trata de una secuencia infinita de números racionales con signos alternos que satisface la relación:

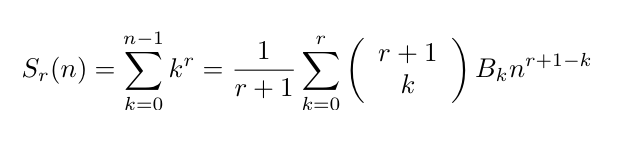
Por ejemplo se tiene:

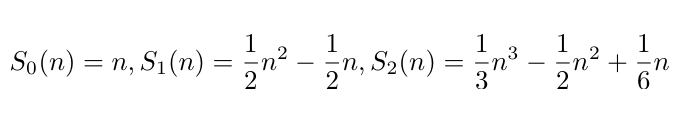
y los primeros valores de la secuencia son los siguientes:

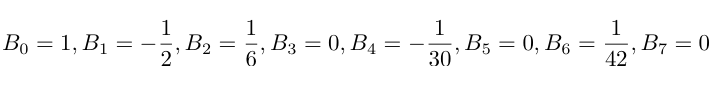
La secuencia de los números de Bernoulli está muy estudiada y quien sienta curiosidad por conocer en qué otros contextos se puede encontrar puede consultar la Enciclopedia OEIS de las secuencias enteras en https://oeis.org/.

Se trata de un archivo que contiene información sobre secuencias de números más o menos conocidos y permite efectuar investigaciones sea por clave sea especificando los primeros valores de la secuencia. En particular, OEIS contiene referencias a la secuencias de los numeradores y denominadores de los números de Bernoulli, identificados por los códigos OEIS A027641 y A027642. ¡Seguramente a Ada le habría gustado utilizar esta enciclopedia y habría quedado encantada!

Comparación con la secuencia de Fibonacci

La secuencia de Bernoulli es una secuencia compleja. Para evidenciar esta característica se puede dar un salto atrás en el tiempo, a 1200, y comparar la secuencia de Bernoulli con la bien conocida secuencia de los números de Fibonacci, introducida por Leonardo Pisano, llamado Fibonacci, de filius Bonaccii, porque era hijo de Guglielmo Bonacci. Se trata de una secuencia infinita de números enteros que comienza con:

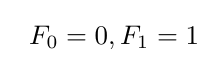y después prosigue con los valores:

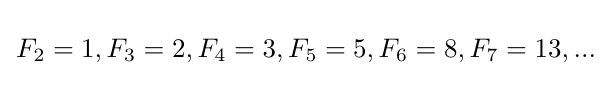Es fácil ver que cada número de la secuencia puede ser fácilmente calculado haciendo la suma de los dos números precedentes. La fórmula es sencilla:

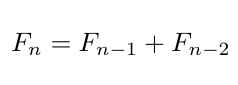Los números de Fibonacci fueron inicialmente aislados para resolver un problema ligado al contenido de las parejas de conejos después de un cierto número de meses: a partir de que una pareja da a luz a una nueva pareja de conejos a la finalización del segundo mes y desde entonces nace una nueva pareja de conejos cada mes. Cada nueva pareja se comporta del mismo modo. No es difícil convencerse de que el número de las parejas de conejos crece exactamente como los números de Fibonacci y que, tras n meses, las parejas son F_n. La secuencia de Fibonacci es mucho más simple que la secuencia de Bernoulli, sin embargo, el cálculo de los números de Fibonacci es a menudo tomado como ejemplo para ilustrar alguna técnica bien conocida de programación y es muy común en informática; en OEIS la secuencia de Fibonacci se identifica con el código A000045.

Numeradores y denominadores de los números de Bernoulli

Volviendo a los números de Bernoulli, el siguiente gráfico ilustra en rojo el número de cifras del numerador y en azul el número de cifras del denominador para los números B_2n con n de 0 a 60.

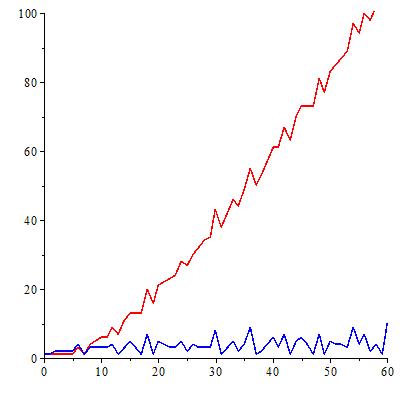
Figura 4 Tendencia del número de cifras del numerador (línea roja) y de cifras del denominador (línea azul) de los números de Bernoulli

Por ejemplo, el número de índice 60 (n = 30 en el gráfico) corresponde a una fracción con número de 43 cifras en el numerador y 8 cifras en el denominador:

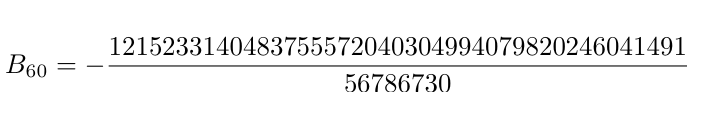
Se trata por tanto de una secuencia con un comportamiento extraño, caracterizada por números con un numerador muy elevado y un denominador relativamente pequeño. Para mayor profundización sobre los números de Bernoulli se recomienda leer el libro Concrete Mathematics de Graham, Knuth y Patashnik (1989).

El algoritmo de Ada

En la nota G, Ada introduce los números de Bernoulli a partir de su función generatriz (exponencial). Se trata de una expresión que en su interior engloba la secuencia entera de números.

De hecho, esta función puede escribirse como una suma infinita en la cual cada término implica un número de Bernoulli diferente, como se ve de la siguiente fórmula:

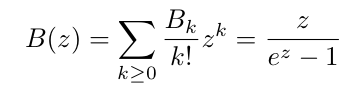
Ada se dio cuenta de que esta expresión no se adaptaba al cálculo con la Máquina Analítica y con la ayuda de Babbage intenta transformarla en la siguiente expresión (que técnicamente es una relación de recurrencia que implica un número finito de números de Bernoulli de índice par a la vez):

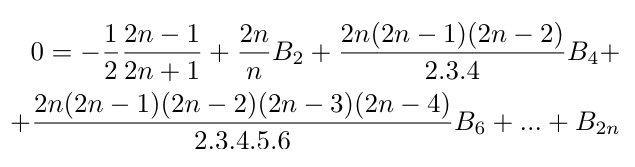
En la práctica, Ada pasa del plano de la función generatriz al de sus coeficientes, utilizando una aproximación típica del análisis moderno de los algoritmos, una parte de la informática que se ocupa del estudio de las propiedades de los algoritmos utilizando instrumentos como las funciones generatrices y las relaciones de recurrencia. La recurrencia de Ada implica n números de Bernoulli a la vez y permite calcular los de índice 2n a partir de los n-1 números precedentes de índice par. Para entender el procedimiento de Ada podemos analizar el cálculo de los primeros números de la secuencia y recordar que la Máquina Analítica es capaz de realizar sumas, sustracciones, multiplicaciones, divisiones, de memorizar el resultado de una operación y de utilizarlo para el cálculo siguiente así como sustituir valores particulares de la variable.

Cuando n = 1, 2, 3 la fórmula de Ada se convierte, respectivamente, en:

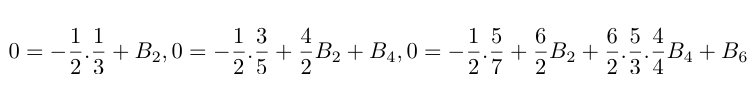
De la primera ecuación se puede obtener B₂ = 1/6, de la segunda ecuación, conociendo ya B₂, se puede encontrar que B₄ = -1/30 y, en fin, de la tercera ecuación, conociendo los números anteriores, se puede encontrar que B₆ = -1/42. El caso n = 4 es todavía más interesante y corresponde exactamente con el ejemplo que está explicado en detalle en la Nota G:

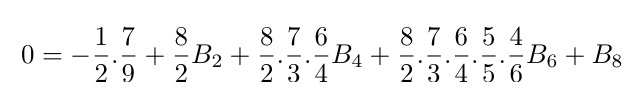Ada identificaba un ciclo principal para calcular la secuencia B₂, B₄, B₆ y B₈, usando un procedimiento equivalente al que se acaba de ilustrar. Por lo que respecta en particular al valor B₈, Ada describía las instrucciones para calcular el primer coeficiente y de ahí los que valen para calcular el segundo. Después Ada observó que cada coeficiente posterior se puede calcular siempre con las mismas instrucciones puesto que los coeficientes implicados se pueden encontrar haciendo el producto de tres factores: por ejemplo, en este caso, tras haber calculado el coeficiente de B₄, el de B₆ se puede encontrar multiplicando este último por los dos factores 5/5 y 4/6. Ada identifica un ciclo interno para el cálculo de los coeficientes implicados y, finalmente, puede obtener B₈ de su fórmula.

En general, en el trabajo de Ada se encuentran por tanto los conceptos de dato, variable, instrucción, ciclo, ciclo anidado y salto condicionado, que están en la base de los modernos lenguajes de programación. Pero se encuentran también consideraciones sobre la importancia de la elección del algoritmo y su número de operaciones, o tarjetas perforadas, necesarias para el cálculo y, por tanto, en las cuentas del algoritmo. También la elección del ejemplo para describir el funcionamiento de la Máquina Analítica es todavía muy actual, de hecho los números de Bernoulli son todavía muy estudiados y las referencias a ellos continúan apareciendo en prestigiosas revistas científicas. Por tanto, definir a Ada como la primera programadora de la historia parece un eufemismo, dado que ella desempeñó un papel bien sea en la elección del algoritmo, en su descripción con la Máquina Analítica y en el análisis de las cuentas. Sin embargo, también en la definición de Ada que a menudo viene reportada en los varios textos disponibles, se encuentra el concepto de Informática percibido de modo erróneo.

Ada olvidada y después descubierta

Babbage murió en 1871 sin haber logrado construir realmente la Máquina Analítica. En los decenios posteriores, el recuerdo de Babbage se atenuó mucho mientras el de Ada se redujo a unas pocas líneas en las numerosas biografías del padre. El recuerdo de la Máquina Analítica reapareció en 1944 durante la inauguración del Harward Mark I, una calculadora electromecánica programable. A la ceremonia fue invitado el canadiense Richard Babbage, bisnieto de Charles. En 1953 se publicó uno de los primeros libros sobre los orígenes del computador (Faster Than Thought) en el cual aparece un retrato de Ada y varios párrafos dedicados a ella. Lentamente se construyó la imagen y el mito de Ada como primera programadora y hechicera de números. Un importante reconocimiento le fue dado en los años ’70 por el Departamento de Defensa americano que bautizó con su nombre un lenguaje de programación que se debería convertir en un estándar para las fuerzas armadas. La versión más reciente del lenguaje de programación “Ada” es del 2012. Este lenguaje se presta a la utilización en cualquier dominio de aplicación, pero tiene características fuertemente orientadas a la seguridad de los códigos y por tanto resulta particularmente adaptado al contexto militar.

¿Por qué las mujeres no se inscriben en Informática y por qué deberían hacerlo?

Existe la convicción común de que es por el estereotipo del nerd, o del genial programador publicitado por la prensa, la televisión o en el cine de los años ’80. Eso termina por alejar a las muchachas de inscribirse en informática.

La informática es una materia creativa e interdisciplinar que ha cambiado el mundo en todos los sectores en los últimos decenios, modificando radicalmente nuestro mundo profesional. Para emprender estudios de informática, las mujeres deben abandonar preconceptos y falsas percepciones sobre esta disciplina. Por otra parte, la informática es sobre todo el estudio de la resolución de problemas y, si es cierto lo que sostienen muchos sociólogos (véase el debate a continuación del espectáculo de V. Patera La fata matematica. Storia della donna che sognò il computer), que las mujeres se inclinan a realizar estudios que ayudan a mejorar la humanidad, la informática y la tecnología informática, si son bien usadas, son un instrumento para mejorar la vida sobre este planeta y las jóvenes podrían satisfacer plenamente esta aspiración.

No es casualidad que en los últimos años, en varias universidades italianas, hayan nacido proyectos para orientar a las chicas hacia esta disciplina. En la Sapienza, por ejemplo, con este objetivo ha nacido recientemente el proyecto http://www.progettonerd.it. También la Universidad Ca’ Foscari se ha embarcado en un camino de este tipo, con un proyecto en el que también participa la Comisión de Igualdad de Oportunidades de la región Veneto. C²