El arte y la ciencia como una descripción del mundo
Desde sus orígenes, tanto el arte como la ciencia han compartido la fascinación por observar del mundo que nos rodea. ¿Qué tan lejanas o cercanas son ambas visiones de la realidad? ¿Podemos cuantificarlas?
Éste es el relato de una búsqueda que emprendimos hace algunos años para contestar tal pregunta. En particular fijamos nuestra atención en van Gogh, dado que los críticos de arte han asociado siempre la palabra “turbulencia” a su obra.

¿Acaso es posible tal asociación? Nuestro relato comienza en Madrid, con los científicos Manuel Torres, de la Universidad Complutense y José Luis Aragón Vera, del Centro de Física Aplicada y Tecnología Avanzada de la UNAM, quienes después de admirar una exposición sobre van Gogh, quedan asombrados de la sensación de movimiento de los cuadros del pintor. Un tiempo después, me uniría a la búsqueda para entender cómo van Gogh había logrado ese efecto. Para ello tuvimos que estudiar turbulencia en fluidos, procesos de imágenes, historia del arte y, desde luego, la biografía de van Gogh. Finalmente, logramos determinar que van Gogh se había adelantado unos 50 años a Kolmogorov en el entendimiento intuitivo del fenómeno de la turbulencia. De hecho, cuando salieron los resultados de la computadora, comparando los cuadros de Van Gogh con la teoría de Kolmogorov, nos produjo una sensación de emoción y miedo. Emoción por encontrar algo nuevo, pero miedo de equivocarnos en algo que parecía muy impresionante. La idea de realizar semejante comparación era de por sí una fuente de gran satisfacción, pero jamás imaginamos lo interesante de los resultados.
En muchos casos la observación de la naturaleza por los artistas precede a su descubrimiento en la ciencia.
Va pues este relato, no sin antes hacer algunos comentarios sobre el arte y la ciencia, para entender por qué nuestra búsqueda era sin duda factible. Es decir, en muchos casos la observación de la naturaleza por los artistas precede a su descubrimiento en la ciencia. La razón de ello es su origen común: observar e interpretar el mundo que nos rodea. De hecho, entre las primeras manifestaciones conocidas del arte podemos citar las pinturas rupestres. Todo mundo sabe que en cuevas alrededor del mundo han sido encontradas escenas cotidianas de caza de animales. Sea cual fuere la razón de esta vocación artística, es claro que la educación de las nuevas generaciones se vería favorecida al explicar de manera visual los hábitos de determinados animales, ayudando en la cacería, así como en a la protección de la tribu. Lo mismo sucede con los cuentos y leyendas que incluyen hábitos de los animales o fenómenos naturales. Lo dicho para la pintura y la literatura puede decirse también para el baile; en México tenemos la danza del zopilote, del venado, del tigre, etc.
Si aceptamos como verosímiles algunas de las ideas anteriores, entonces no será difícil pensar en que las primeras manifestaciones artísticas trataban de recrear de manera fiel al mundo natural, especialmente en la pintura. Un caso singular lo constituye la música; al parecer no reproduce a la naturaleza, sin embargo, su estructura es muy similar a los ruidos naturales con características fractales. En el siglo XX se logran conseguir medios para reproducir fielmente al mundo que nos rodea, y como resultado, el arte deja de centrarse en el realismo para emprender otros caminos.
La ciencia, al igual que el arte primitivo, comienza básicamente con una descripción del mundo natural.
La ciencia, al igual que el arte primitivo, comienza básicamente con una descripción del mundo natural. Así, la ciencia no trata de responder por qué cae una piedra, más bien dice cómo cae, es decir, cuánta distancia recorrerá en un tiempo dado y cuál será su velocidad, describiendo esta relación en un lenguaje universal: la matemática.
Desde luego, existen diferencias entre el arte y la ciencia. Podría argumentarse por ejemplo que la ciencia tiene un elemento de lógica que no está presente en el arte. Sin embargo, la lógica no siempre es un buen camino para la ciencia. Artistóteles logró, mediante razonamientos lógicos, atrasar el desarrollo de la física durante varios cientos de años. La mecánica cuántica, usada para describir la física del mundo subatómico, es un desafío permanente a la lógica. Así, debemos remarcar que, tal y como atinadamente dijo Leonardo Da Vinci, la naturaleza es la mejor maestra. Esa es la característica principal de la ciencia, su método experimental.
Curiosamente, podría pensarse entonces en que los científicos usan un pensamiento matemático o verbal para describir y entender la realidad del mundo. Diversos comentarios de destacados científicos muestran que ese no es el caso, y que de hecho, las formas no verbales de pensamiento son las mas importantes para su trabajo [Penrose]. Los científicos más influyentes, generalmente han imaginado una nueva realidad antes que la lógica o el experimento mostrara su existencia.
Pongamos tres ejemplos significativos:
- “Las palabras o el lenguaje, ya sea escrito o hablado, no parecen jugar ningún papel en mi mecanismo de pensamiento. Las entidades físicas que parecen servir como elementos del pensamiento, son ciertos signos e imágenes más o menos claras que pueden reproducirse y combinarse voluntariamente. Los elementos mencionados son de tipo visual y muscular. Las palabras u otros signos tienen que buscarse laboriosamente en una segunda etapa, cuando el juego asociativo está suficientemente establecido y puede ser reproducido a voluntad.” A. Einstein.
- “No pienso tan fácilmente en palabras como en otras formas. Habiendo llegado a resultados claros y satisfactorios para mí, cuando trato de expresarlos en lenguaje siento que debo colocarme en un plano intelectual muy distinto”. F. Galton .
- “Coincido con Schopenhauer: las ideas mueren cuando se encarnan en palabras”, Hadamard.
La habilidad para imaginar nuevas realidades está más relacionada con el juego, la modelización, la abstracción, la armonía, la formación de patrones, la capacidad de hacer analogías y la extrapolación, que en pocas palabras, son características asociadas con el arte. Tal vez por ello el arte ha producido resultados científicos importantes sin haberlo sabido, así como también la ciencia ha nutrido al arte, especialmente durante los últimos cien años.

El ejemplo más simple de lo anterior aparece en las simetrías de los patrones geométricos que se pueden formar mediante la repetición de un motivo básico. Los patrones han sido utilizados por casi todos los pueblos civilizados para recubrir pisos con baldosas, para decorar tejidos o paredes. En la figura 1 tenemos un ejemplo de mosaico usado como piso en la ciudad romana de Pompeya.
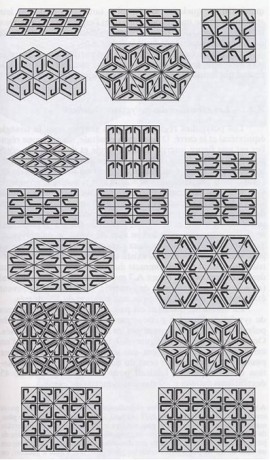
Las árabes descubrieron que existen sólo 17 formas fundamentales de llenar un plano, las cuales aparecen en la figura 2. Fue tal su impresión que estas 17 formas aparecen como estructura básica de los mosaicos del Alambra de Granada. Varios siglos después, el problema cobró importancia en la cristalografía, la cual trataba de entender todas las formas posibles que puede tener un cristal, como por ejemplo el azúcar o la sal, los cuales se forman mediante la repetición de celdas de átomos, de la misma manera en la que una pared se forma apilando ladrillos. Finalmente, no sólo se confirmó el descubrimiento de los árabes, sino que se extendió a patrones tridimensionales para los cuales hay 230 simetrías posibles. El lenguaje usado para describir estas simetrías es la llamada teoría de grupos. Este tópico es muy extenso para discutirlo aquí, pero solamente diremos que el manejo de la simetría es una constante en la naturaleza y por lo tanto en la ciencia y en el arte. Tan es así, que aún las teorías más sofisticadas de los físicos, como la teoría estándar que explica la formación de las partículas subatómicas, se descubrió pensando en analogía con las simetrías de un sólido platónico llamado octaedro.
Podría pensarse que la ciencia del siglo XX, con su alto grado de desarrollo, podría estar exenta de encontrar resultados en terrenos pisados por artistas. Como veremos, éste no es el caso. Para ello, exploraremos el territorio del caos y la turbulencia, que recién fueron entendidos a mediados del siglo XX. Nuestro camino nos llevará a mostrar que el pintor holandés Vincent van Gogh (1853-1890) fue capaz de reproducir de manera bastante exacta las propiedades básicas de la turbulencia de fluidos.
Caos, turbulencia y autosimilaridad
Al estudiar la naturaleza, lo primero que han comprendido todos los pueblos es el orden. Así, los ciclos del día y la noche, las fases de la luna, las estaciones, eclipses, mareas, etc., siempre fueron observados con gran atención por sus implicaciones prácticas, y en muchos casos, fueron integrados a las religiones de cada cultura.
En todas las culturas también se ha entendido que existen otros fenómenos que no presentan regularidades tan claras, como tormentas, inundaciones, rayos, etc. Recién hasta mediados del siglo XVIII se empezó a poder describir este “desorden” en términos matemáticos. Ello basado en la observación de los juegos de azar. Pero es a mediados del siglo XX cuando la ciencia se enfoca a entender cómo del orden se pasa al desorden. ¿Fue ajeno el arte a esta pregunta?

Para responderla, hablemos de otro fenómeno que había sido estudiado de manera intuitiva por algunos artistas y científicos, pero que recién empezó a entenderse durante la segunda década del siglo XX. Este fenómeno los vemos todos los días al abrir la llave para lavarnos las manos. Si se abre la llave muy poco, el agua parece seguir un patrón con una forma fija que no cambia con en el tiempo, como se muestra en el panel izquierdo de la figura 3. Al abrirla un poco más (panel derecho), llega un momento donde el flujo se vuelve errático y cambia de forma constantemente; a eso se le llama turbulencia.

La turbulencia ha sido observada por muchos artistas, entre ellos Leonardo da Vinci (figura 4) o, por ejemplo, el pintor japonés Hokusai Katsushika (figura 5).

En ambos cuadros se puede notar una observación importante de los autores: la auto similaridad. Este fenómeno es también una forma de simetría, conocida como invariancia de escala o fractalidad. Su importancia radica en que aparece en los fenómenos conocidos como caóticos, es decir, en procesos que se vuelven “impredecibles” a largo plazo. La autosimilaridad consiste en que un objeto o fenómeno se ve igual cuando cambiamos la escala en que lo vemos. Por ejemplo, si vemos una rama de un árbol notamos que su aspecto es similar a la del árbol mismo, aunque a diferente escala.
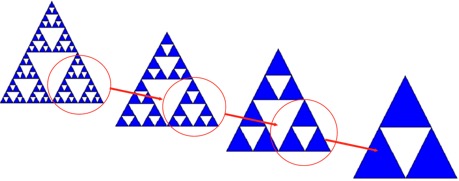
En la figura 6 mostramos un objeto con una autosimilaridad muy clara. Este objeto se conoce como la galleta de Sierpinsky. La galleta, como un todo, está formada por versiones escaladas de sus partes.

Un análisis detallado de las figuras 4 y 5 revela que en ellas hay remolinos de agua que son casi idénticos entre sí, excepto por el tamaño. Esta característica es la que está detrás de un flujo turbulento, como se observa en las figuras 7 y 8 que corresponden a fotos de turbulencia real. Obsérvense los remolinos a diferentes escalas; familiares para cualquiera que observe espirales en un café con crema.
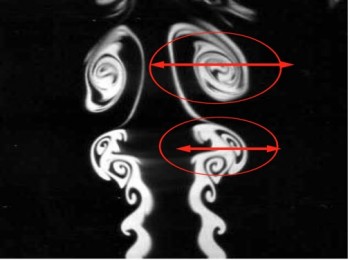
La figura 8 es especialmente reveladora, en ella se aprecia cómo los remolinos grandes se van convirtiendo en otros cada vez mas pequeños hasta desaparecer totalmente.
Las ideas centrales de los físicos acerca de la turbulencia se basan justamente en la observación de que existe una cascada de remolinos autosimilares, cada vez más pequeños hasta llegar a una escala donde éstos desaparecen. Como hemos visto, estas observaciones aparecen repetidamente en diversos autores. Sin embargo, el artista con el cual más se ha asociado la palabra turbulencia es van Gogh. C2





Hilda -
Excelente artículo!
Muy interesante y escrito en forma muy didáctica.