Lo óptimo y lo bello

Ciencia

Lo óptimo y lo bello

6 septiembre, 2016
|
POR Rosa María Herrera
|
0 COMENTARIOS
|
Like 0
|
423

Si la naturaleza es la respuesta. ¿Cuál era la pregunta?
Wagensberg

Local y global: diversos modos útiles de interrogar a la naturaleza

Se detecta la presencia de un objeto celeste no conocido situado en A en un tiempo determinado; podría ser un cometa capturado por el Sistema Solar o tal vez un asteroide de la población situada entre las órbitas de Marte y Júpiter. Por su ubicación en la dirección de la trayectoria del sistema Tierra-Luna (T) tal vez podría ocasionar algún problema. Vamos a ver cómo habría que afrontar esta eventual y desagradable situación.

¿Cuál es el siguiente lugar por el que pasará?

Newton quizá nos orientaría preguntándonos: conocidas las condiciones iniciales de posición y tiempo ¿cuál es el siguiente lugar por el que pasará? Pero hay otras preguntas que representan una visión levemente diferente y nos ayudan también. Por ejemplo, Hamilton quizá nos diría: para ir desde el punto A donde el objeto celeste se ubica, hasta el punto T donde se halla el “blanco” involuntario, ¿qué camino hay que seguir?

Observación de algunos principios de optimización en la naturaleza

Los primeros estudios vienen de más lejos. Herón de Alejandría (s.I. d.C.), geómetra y seguramente hábil experto mecánico, se interesó por estudiar algunas curiosidades de las formas relacionadas con la óptica. Para ello observaba las propiedades de los rayos de luz sirviéndose en ocasiones de ingeniosos juegos con espejos. De este modo se dio cuenta de que para comprender lo que se veía en ellos era necesario conocer cómo funciona la luz al reflejarse. Así, llevó a su libro la Catoptrica una observación que se puede expresar más o menos así: “un rayo de luz se refleja sobre un espejo siguiendo el camino más corto, independientemente del punto en que la luz incida sobre el espejo; este resultado se obtiene a partir de la observación geométrica de la igualdad de los ángulos de incidencia y de reflexión” [1].

Damos ahora un gran salto hacia delante en el tiempo y nos situamos en la edad moderna, y para entender un poco mejor el proceso nos detenemos un instante en Fermat (1601-1665), quien en 1662 estableció que la luz sigue siempre la trayectoria en la que invierte el mínimo tiempo.

Posteriormente, Maupertuis (1698-1759), Euler (1707-1783), Lagrange (1736-1813), Gauss (1777-1855) y algunos otros formularon algunas buenas generalizaciones que tienen gran interés para resolver diferentes problemas haciendo cierto tipo de preguntas que son compatibles con la idea (que tiene un aire metafísico [2]) de un principio de simplicidad y economía de la naturaleza que se había ido desarrollando previamente en el transcurso de los siglos, y cuyos primeros rasgos se encuentran en las antiguas leyes que emanan de la óptica.

El principio de mínima acción

Una de estas generalizaciones que nos resulta especialmente interesante a los aficionados a la mecánica es el principio de Hamilton (1805-1865) de acción estacionaria o de mínima acción [3]: consideremos una partícula (masa puntual o punto material) en un campo gravitatorio uniforme, moviéndose de un punto A hacia un punto B en un cierto tiempo, y que describe una trayectoria determinada.

Sin modificar las condiciones físicas de dicha partícula, no es difícil imaginar alguna otra trayectoria posible entre esos dos puntos arbitrariamente elegidos, A y B, en la cual se invierta el mismo tiempo. Pues bien, si se calcula en cada instante la diferencia entre la energía cinética y la energía potencial, y se halla la media de esta diferencia a lo largo de la trayectoria imaginaria, entonces, el resultado es un número que siempre es mayor que el número similar encontrado para la trayectoria que la partícula sigue en su camino real.

Esto significa, por ejemplo, que la partícula pasa por el punto más bajo a la mayor velocidad, porque en él la energía potencial es menor.

Así, vemos que este principio expresa en términos de máximos y mínimos, o de puntos estacionarios y críticos (formulación variacional), a la segunda ley de Newton. Dicho de otro modo, las leyes fundamentales de la Mecánica Clásica (que son locales) se pueden expresar considerando que la acción en el curso del movimiento es estacionaria (o al menos forzosamente minimal). Es decir, invariante por variación infinitesimal del camino seguido.

Este principio ha suscitado muchos comentarios teleológicos, pues los sistemas mecánicos se comportan como si su evolución estuviese encaminada a optimizar esta misteriosa “acción” (S), definida como:

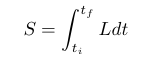
Designando como L (lagrangiano) a una función definida de la siguiente forma:

donde Ec es la energía cinética y Ep la energía potencial, L depende en cada instante de la configuración y la velocidad del sistema. Sabiendo que un punto de una cierta función es estacionario si la derivada de dicha función en el punto es cero,

entonces,

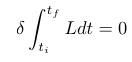
Aquí la sutileza de la comprensión está en la relación que existe entre la ecuación diferencial del movimiento correspondiente a la segunda ley de Newton (ecuación diferencial), y la acción de Hamilton (ecuación integral):

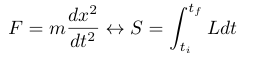
En este sentido, la pregunta de cada una de las dos visiones es distinta, con un diferente enfoque para resolver el mismo problema (en las que las respuestas deben ser la solución del mismo).

Los principios variacionales

Les principes variationnels sont la forme mathematique du superlatif.
Los principios variacionales son la forma matemática del superlativo (J-L Basdevant).

El principio de Herón del camino más corto, el de mínimo tiempo de Fermat y el de mínima acción de Hamilton que acabamos de señalar someramente y de manera sencilla, forman parte de un tipo de principios físicos denominados principios variacionales. Los principios variacionales están ligados a una descripción global de la evolución del sistema estudiado entre dos sucesos fijos que vienen caracterizados por sus posiciones y sus tiempos.

La mayoría de las leyes físicas se expresan en forma de ecuaciones diferenciales.

La forma inicial de la mayor parte de las teorías físicas clásicas explica un fenómeno mediante leyes de tipo local, como las leyes de Newton de la mecánica, las de Maxwell del electromagnetismo, o las de la termodinámica. Éstas y la mayoría de las leyes físicas se expresan en forma de ecuaciones diferenciales; y los matemáticos nos enseñan que en realidad muchas ecuaciones diferenciales admiten una visión global, es decir una formulación variacional, que podemos utilizar para trabajar también como con nuestras ecuaciones diferenciales procedentes de la física.

Una curiosidad histórica

Por convención se suele considerar un punto de partida [4] del cálculo de variaciones en la propuesta de estudio que en 1696 Johann Bernouilli (1667-1748) hizo sobre el problema de la braquistocrona [5] a varios científicos relevantes de su tiempo; de forma anónima remitió el problema a Leibniz, Jakob Bernouilli, Newton, L’Hôpital y alguno más. Veamos el problema:

Una partícula se mueve desde un punto A hasta uno B por acción de la gravedad siguiendo una línea. El tiempo empleado depende de la trayectoria elegida, la pregunta planteada es: ¿qué trayectoria debe seguir la partícula para que el tiempo invertido sea mínimo?

Tanquam ex ungue leone (reconozco las garras del león).

Siguiendo el primer impulso responderíamos tal vez que la recta que une los puntos A y B, o quizá un arco de circunferencia que pase por ellos. Sin embargo, la solución es un arco de cicloide [6], y la encontraron varios matemáticos, entre ellos y de manera rápida, según se dice, Newton. La historia es bastante rocambolesca y aquí está muy resumida, pero parece que al leer la respuesta enviada anónimamente por Newton, Johann pronunció la frase Tanquam ex ungue leone (reconozco las garras del león), identificando así al científico británico.

Breve nota final

También en el siglo xx y en nuestros días, el trabajo con el principio de mínima acción sigue generando profundo interés. Físicos notables como Dirac (1902-1984), Feynman (1908-1988) y algunos otros, que trabajaron en Mecánica Cuántica se interesaron por el principio de mínima acción y contribuyeron a proporcionar una explicación que se apoya en el cálculo de la interferencia de funciones de onda y su fórmula de la fase estacionaria.

Richard Feynman se interesó, desde su época de estudiante, por este principio, y siempre lo encontró fascinante. Existen varias anécdotas de la relación entre el físico y el principio, que seguramente muchos conocerán. Algunos comentarios se pueden encontrar en su célebre curso de física; en un momento determinado se hace la pregunta retórica de si realmente la partícula escoge la mejor entre todas las trayectorias posibles (la que significa la mínima acción), y si es así, si al introducir obstáculos se produciría un fenómeno similar a la difracción, para concluir que en efecto es lo que ocurre [7].

En los últimos decenios se está trabajando en un nuevo principio de mínima acción interesante en la dinámica clásica, en la que los objetos minimizados ya no son caminos individuales, sino medidas destinadas a comprender fenómenos sutiles de dinámica global. C²

Bibliografía

Feynman, R.P. The Feynman Lectures on Physics, 1964
Lemons, D.S., Perfect form Variational Principles, Methods, and Applications in Elementary Physics, Princenton Univ. Pres. New Jersey, 1997
Martin Robin, F., Histoire du Principe de Moindre Action, Vuibert, Paris, 2009
http://www-history.mcs.st-and.ac.uk/

Referencias

[1] En tiempos pasados consideraban que los ojos emiten rayos de luz, a velocidad infinita, y siguen la línea más corta.

[2] Al menos inicialmente, rápidamente adquirió un estatus matemático muy potente.

[3] La primera definición de acción que dio Maupertius reza así: el producto de la duración de un movimiento por el doble de la energía cinética (vis viva, como se denominaba entonces).

[4] Parece que en realidad el primer problema significativo del cálculo de variaciones fue propuesto por Newton en su libro 2º de los “Principia…” y estudiaba la forma que debía tener una superficie de revolución moviéndose en un fluido a v = cte. a lo largo de su eje para ofrecer una resistencia mínima.

[5] https://es.wikipedia.org/wiki/Curva_braquist%C3%B3crona

[6] https://es.wikipedia.org/wiki/Cicloide

[7] Por ejemplo: Is it true that the particle looks at all the other possible trajectories? […] Feynman Lectures on Physics R. Feynman (1964).

Sobre el autor

Rosa María Herrera

Profesora e Investigadora en UPM, España

Estudió física. Su interés es sobre la estabilidad dinámica del Sistema Solar y los sistemas hamiltonianos de baja dimensión. Se interesa además por los principios variacionales en física y la divulgación científica.