En el mundo macroscópico medir fuerzas ha sido uno de los pilares de la experimentación científica y base del desarrollo tecnológico. En 1687, Newton, en su obra “Principios matemáticos de la filosofía natural”, acuñó su unidad de medida: El Newton [N], que se define como la fuerza necesaria para mover un cuerpo de 1 kg de masa a una aceleración de 1 m/s² (1). Desde la antigüedad, ha sido esencial para el hombre aprender a controlar fuerzas para la manipulación de metales en la construcción de herramientas; o en el diseño y fabricación de cohetes espaciales, lo que ha permitido llevar humanos al espacio y establecer redes de comunicación satelital. El control y medición de las fuerzas ha posibilitado el desarrollo tecnológico actual.
Existen otras áreas del conocimiento donde medir fuerzas es relevante, y que en su momento representaron retos científicos importantes debido a su complejidad. Un ejemplo es el mundo microscópico, en particular el biológico. Conocer propiedades físicas en esta área podría ayudar al estudio y diagnóstico de enfermedades e incluso a generar terapias médicas. Determinar la fuerza necesaria para deformar la membrana de una célula sana y comparar esas propiedades en células con alguna enfermedad permitiría diseñar fármacos especializados. El estudio de los virus es una herramienta clave para combatir enfermedades en seres humanos, animales y plantas, provocadas por dichos agentes. El entendimiento de los organismos vivos y sus procesos evolutivos podrían emplearse en la medicina, por ejemplo en el encapsulado de fármacos. Además de los procesos moleculares y la velocidad de su replicación en células hospederas, la ciencia se ha ocupado en conocer las fuerzas necesarias para la formación de las cápsides (2), así como la que requieren los motores moleculares en virus para el empaquetamiento de su material genético (3).
A pesar de la necesidad imperiosa de medir fuerzas, hay que considerar la escala de las fuerzas de las que hablamos: picoNewtons. Es decir, una millonésima parte de una millonésima de Newton (1pN = 0.000000000001 N). Su estudio y medición ha necesitado el diseño de metodologías y técnicas extremadamente sensibles, representando un reto científico y tecnológico. También es de interés que la técnica experimental a emplearse en esta área de investigación sea flexible en diferentes escenarios, como el estudio de células vivas en un medio acuoso. Con esto parecería que se necesita una técnica casi esotérica para manipular micro-objetos con una fuerza muy pequeña y preferiblemente sin contacto. Este es el tipo de aplicación que proporcionan las pinzas ópticas, convirtiéndose así en una poderosa herramienta de análisis y estudio experimental.
Fue Arthur Ashkin de los laboratorios Bell, quien en la década de los 70 revolucionó la forma en la que se miden las fuerzas microscópicas, al demostrar el fenómeno físico que dio origen a las pinzas ópticas (4). La relativa sencillez de su construcción y el fácil entendimiento de su funcionamiento logró que esta herramienta fuera aplicada rápidamente a las áreas biológicas y en la biofísica, por lo cual se le otorgó el Premio Nobel de 2018 por ““the optical tweezers and their application to biological systems”, junto con Donna Strickland y Gérard Mourou por sus investigaciones sobre los Pulsos Láser.
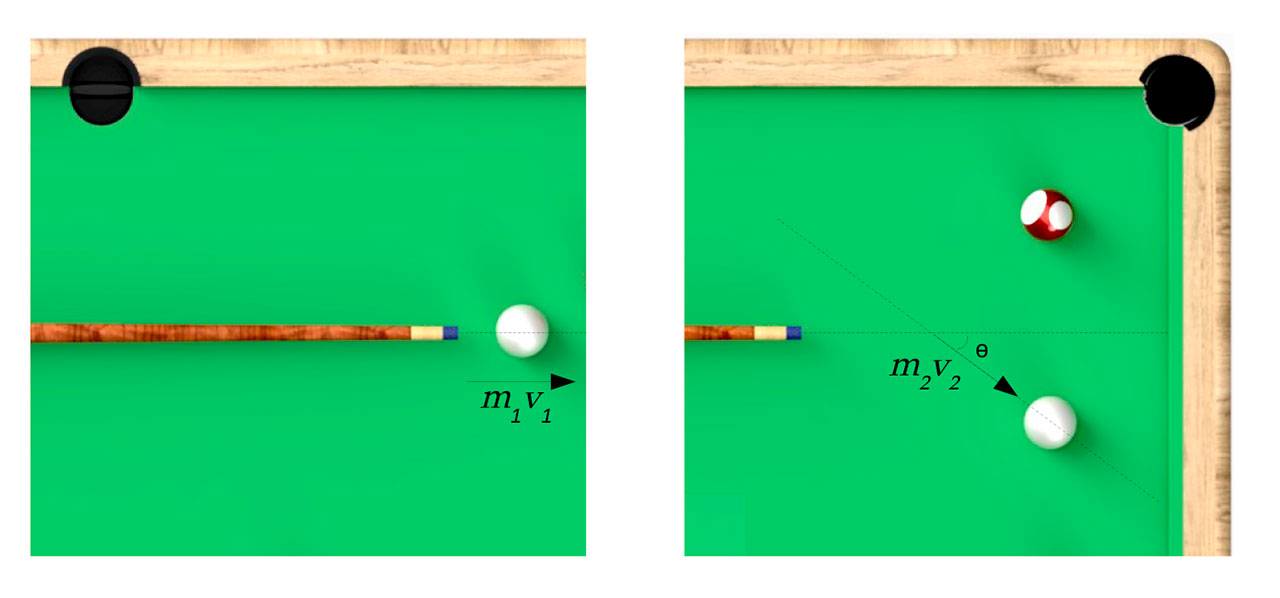
Con el fin de ejemplificar el origen físico de las pinzas ópticas, pensemos en un experimento similar al mostrado en la figura 1a. Una bola de billar es impulsada a una zona no visible por el espectador (en este caso en dirección horizontal), para después salir en una dirección completamente diferente a la que venía. El observador puede deducir que alguna fuerza fue la responsable del cambio de dirección, y que posiblemente fue originada por un choque con algún objeto en la zona no visible, como lo muestra la figura 1b. En términos de física, se dice que el momentum de la bola de billar cambió debido a una fuerza externa.
El momentum se define como la masa del objeto multiplicada por su velocidad. Si se analiza no sólo una bola de billar, sino todo el sistema (incluyendo al objeto que modificó su trayectoria y que en el caso de la figura 1 es otra bola de billar), las leyes de la física implican que el momentum total se debe conservar al ser un sistema aislado. Nótese que al inicio del experimento no hay velocidad en la dirección “y”, lo que implica que el cambio del momentum de la bola de billar observado debe equipararse al que obtuvo el otro cuerpo, de tal manera que el momentum se conserva, lo que sólo se logra con un cambio en la dirección de la bola. En el ejemplo de la figura 1, el objeto con el que chocó la bola en cuestión debería salir en la dirección opuesta para mantener el momentum en la dirección “y” nulo.
El lector pondrá su imaginación a volar al enterarse de que el fotón, el elemento cuántico mínimo de la radiación electromagnética, también cuenta con un momentum asociado. De forma similar al caso de la bola de billar, cuando un fotón golpea una superficie reflejante como un espejo, cambiará su momentum, y por las leyes de conservación, el espejo sentirá una fuerza que lo empuja. El mismo efecto se nota cuando un haz se refracta en una superficie, como un vidrio o un diamante. Esto es similar a un gas atómico en un recipiente en el que los átomos golpean las paredes del contenedor y se reflejan hacia dentro, dando origen al fenómeno que se conoce como presión. A diferencia del momentum clásico, el momentum del fotón depende del color de la luz en cuestión, y no de su masa o velocidad (dado que el fotón no tiene masa y siempre lleva la misma velocidad). Sin embargo, el momentum del fotón tiene una magnitud muy pequeña por lo que intentar tirar un espejo, al iluminarlo con una lámpara es una tarea inútil, y asimismo tratar de construir un rayo elevador como el que usan los OVNIS, en el argot popular, es fantasioso. Se requeriría una cantidad de energía tan alta que quemaría al objeto en cuestión. En cambio, esta limitante se ve reducida en el mundo microscópico, que es el que interesa.
A diferencia de la luz emitida por un foco, la que proviene de un láser tiene características específicas: todos los fotones o rayos de luz del láser corresponden a una cierta longitud de onda o color, llevan una misma dirección de propagación y a su intensidad, que es la cantidad de fotones por escala de tiempo que emite, se le puede asociar un gradiente. En cambio, la luz que despide un foco cualquiera de casa, son fotones de todos los colores y la dirección de propagación es radial a su fuente.
Ashkin usó un haz de luz láser en una suspensión acuosa de partículas micrométricas y se dio cuenta que éstas, al acercarse al rayo de luz, se veían empujadas en la dirección de propagación del láser. En este caso el cambio del momentum del fotón es originado por la refracción de los fotones en la interfaz entre la partícula y el medio que la rodea, y que sigue la ley de Snell. Poco tiempo después, usando un objetivo de microscopio, Ashkin pudo realizar una manipulación total de la partícula atrapada cerca del foco del objetivo de microscopio. Al determinar la fuerza con la que el haz de luz atrapa a la partícula, Ashkin encontró que era del orden de pico-newtons para haces de luz láser de unos cuantos miliwatts (mW). Como referencia, los apuntadores láser que se emplean para presentaciones tienen una potencia de entre 4 o 5 mW, así que en principio esta potencia es suficiente para atrapar partículas micrométricas con la condición de que se enfoque el láser en un área del tamaño de micras. Las características de una trampa óptica se verán más adelante.
Además se encontró que la fuerza de restitución que siente la partícula se modela como un resorte de Hooke, es decir, que es proporcional al desplazamiento de la partículas respecto al centro de la trampa, por lo que el parámetro que caracteriza a la pinza óptica es una constante del resorte. De manera similar, para potencias de láser de unos cuantos mW, se obtiene una constante de pN sobre micrómetro, lo que indica que es necesaria una fuerza de este orden para mover la partícula un micrómetro del punto central de la pinza. En el video 1 se muestra la representación artística de la pinza óptica, al comparar lo que sucede con la partícula cuando se desplaza del centro de la trampa con una partícula pegada con un resorte. Este movimiento es idealizado y solo pretende ejemplificar la equivalencia mecánica. En un experimento real, la partícula no se mueve armónicamente, sino que tiene un movimiento errático proveniente del movimiento Browniano, pero siempre regresando al centro de la trampa.
Se podría enumerar la gran cantidad de experimentos que los científicos han realizado en décadas recientes. En su lugar se muestran experimentos realizados en instituciones mexicanas.
En el video 2 se presenta el efecto que tiene una pinza óptica en 3 partículas de plástico de 2 micras de diámetro cada una. Inicialmente, el haz de luz láser se encuentra apagado, por lo que las 3 partículas son libres de moverse y presentan movimiento browniano, típico de partículas microscópicas en soluciones acuosas. Al encender el haz de luz, las 3 partículas se juntan y se mantienen moviéndose alrededor del punto focal de la pinza óptica; así se demuestra que el origen del atrapamiento es la interacción de la partícula con el láser al apagar y encenderlo continuamente. El experimento fue realizado en el laboratorio de materiales blandos de la División de Ciencias e Ingenierías de la Universidad de Guanajuato.
Para explicar el siguiente experimento, se destaca que la única característica que debe tener el objeto al ser atrapado es un índice de refracción mayor que el del medio que la rodea, para que se produzca el fenómeno de refracción en el cual el fotón cambie su momentum, y por lo tanto el objeto sienta una fuerza debido a la conservación del momentum que el fotón inicialmente llevaba. Por ello es posible manipular sistemas biológicos de manera directa, pues tienen un índice de refracción mayor que el medio acuoso que las rodea. Un ejemplo de esta manipulación se muestra en el video 3, donde un espermatozoide es manipulado por la trampa óptica. Esta demostración del atrapamiento de sistemas biológicos fue efectuada en el Instituto de Física de la Universidad Autónoma de San Luis Potosí, donde el programa de Biofísica contempla la realización de estos experimentos.
Gracias a Arthur Ashkin se sabe que la luz es capaz de manipular partículas microscópicas sin contacto con fuerzas muy pequeñas. Así fue posible usar las pinzas ópticas para medir fuerzas en el mundo microscópico, y en particular en temas biológicos, con gran impacto no solo en el conocimiento científico adquirido, sino también en aplicaciones tecnológicas. Además se mostraron un par de ejemplos de experimentos realizados en laboratorios nacionales donde se realizan investigaciones científicas usando pinzas ópticas (5).
Estas aplicaciones permiten medir y aprender sobre las características físicas de células, partes celulares, virus, liposomas, etcétera. C2
Bibliografía
(1) Britannica, The Editors of Encyclopaedia. “Newton”. Encyclopedia Britannica, 17 Dec. 2020, https://www.britannica.com/science/newton-unit-of-measurement. Accessed 21 April 2021.
(2) Hagan M. F. (2014). Modeling Viral Capsid Assembly. Advances in chemical physics, 155, 1–68. https://doi.org/10.1002/9781118755815.ch01
(3) Smith, D. E. et al. The bacteriophage φ29 portal motor can package DNA against a large internal force. Nature 413, 748–752 (2001). Bustamante, C., Bryant, Z. & Smith, S. Ten years of tension: single-molecule DNA mechanics. Nature 421, 423–427 (2003). https://doi.org/10.1038/nature01405
(4) Ashkin, A. (1970). Acceleration and trapping of particles by radiation pressure. Physical review letters, 24(4), 156.
(5) Posadas García, Y. S. (2016). Manipulación neuronal por medio de pinzas ópticas.



