Rutas para viajar por el Sistema Solar

Ciencia

Rutas para viajar por el Sistema Solar

18 octubre, 2015
|
POR Rosa María Herrera
|
0 COMENTARIOS
|
Like 0
|
996

He examinado la cuestión bajo todos sus aspectos, la he abordado resueltamente, y de mis cálculos indiscutibles resulta que todo proyectil dotado de una velocidad inicial de doce mil yardas [1] por segundo, y dirigido hacia la Luna, llegará necesariamente a ella. Tengo, pues, distinguidos y bravos colegas, el honor de proponeros que intentemos este pequeño experimento.
“De la Tierra a la Luna” (J. Verne)

Las naves colgaban del cielo casi del mismo modo en el que los ladrillos no lo hacen. “Autopistas galácticas”
(D. Adams)

Figura 1. a) “Principia Matematica Philosphiae Naturalis” de I. Newton

En la obra capital de Isaac Newton (1642-1727) “Principia Matematica Philosophiae Naturalis” (Principios matemáticos de la filosofía natural), de 1687, se recoge la siguiente idea: El mismo principio físico rige el movimiento de una bola de cañón lanzada desde la cima de una montaña que el movimiento orbital. De hecho, la trayectoria de una bala de cañón (o de una pelota lanzada) es un fragmento de una elipse, tan pequeñito que parece una parábola.

La idea manifestada por Newton quizá haría pensar que para poner en órbita un proyectil bastaría con lanzarlo como una bala de un cañón situado en la cumbre de un monte, cuanto más elevado mejor. Pero esta concepción, sin refinar y sin completar, teniendo en cuenta las leyes de la naturaleza que la física describe, encierra bastantes errores básicos y resulta algo ingenua, aún suponiendo que fuese posible que algún hábil fabricante encontrara la manera de construir un cañón de tanto alcance.

Figura 2. Una parte de la elipse coincide con la trayectoria de una parábola en las proximidades del Sol, ilustrando la trayectoria de un cometa -dibujo extraído de un curso de astronomía de F. Tisserand (1845-1896)-.

Por ejemplo, el entusiasta debería contar con la resistencia que ofrece el aire que, por una parte frenaría el movimiento del proyectil en no demasiado tiempo, pero además el calor producido en la fricción lo convertiría en vapor rápidamente. En fin, no hace falta ahondar demasiado, la realidad inmediata muestra inviable esta posibilidad.

Dado que las expectativas de poner un objeto en órbita por el método citado parecen poco realistas, a pesar de que son muy divertidas, vamos a observar algunas características esenciales del movimiento de los astros y las comparamos con las que deberían tener los vuelos espaciales diseñados por humanos; y así nos planteamos con la aportación de algunos elementos más realistas las posibilidades de llevarlos a la práctica.

Tres son multitud…

En sentido clásico, los asuntos “mecánico-matemáticos” están bajo control (relativamente), mientras se puedan manejar considerando dos cuerpos (el caso de una estrella y un planeta, un planeta y un satélite, o la Tierra y un cohete lanzado). En realidad son complicados casi siempre, pero conocidos y abordables.

La dinámica es mucho más difícil en el caso de que tres (o más) cuerpos interaccionen gravitatoriamente; por ejemplo, el Sol, un planeta y un satélite. Es el célebre “problema de los tres cuerpos”.

Las ecuaciones son de un planteamiento relativamente sencillo.

Éste en principio es un problema de origen matemático y forma parte de una situación más general “el problema de los n cuerpos” que matemáticamente se formula como un sistema de ecuaciones diferenciales ordinarias no lineales que propuso Newton en su obra principal (antes citada) para hacer un modelo de nuestro Sistema Solar. Las ecuaciones son de un planteamiento relativamente sencillo, pero su resolución es muy difícil y ha ocupado a algunas de las mejores mentes matemáticas de los últimos siglos, sin encontrar solución analítica general.

En algunos casos particulares, como en el nuestro con n = 3 se han encontrado algunas soluciones para casos especiales, que además de bonitas, son muy útiles como referencia teórica para estudiar algunos aspectos de cierto tipo de órbitas que impliquen 3 cuerpos moviéndose en el Sistema Solar, como son los casos de algunas trayectorias de dispositivos diseñados en la Tierra.

Resumiendo, aunque no se ha hallado una solución general, las soluciones particulares que se han encontrado aportan comprensión de algunos movimientos orbitales, útiles para entender la naturaleza de nuestro Sistema Solar, y para emplearlas de modo inteligente en la astrodinámica de vuelos interplanetarios.

En el caso de un cuerpo de masa muy pequeña como una nave espacial terrestre, la dinámica que se genera es muy interesante y bonita. Y algunas soluciones son un soporte teórico para diseñar con aprovechamiento la maniobra de “asistencia gravitatoria” que propicia un cambio de trayectoria acelerando o frenando una nave espacial utilizando el campo gravitatorio de un planeta o un satélite y ayudándonos a solventar el problema de la energía necesaria para el movimiento. Son los llamados encuentros gravitacionales, cuya importancia se irá comprendiendo poco a poco.

Detalles asociados con la propulsión de los vehículos espaciales

El problema de la energía necesaria para realizar un viaje por el Sistema Solar es un ejemplo típico del caso de la masa variable.

Nuestra Tierra cada vez es más gordita, ya que material de diverso origen incide sobre ella, y eso hace que se incremente su masa, pero al Sol y a las naves espaciales les ocurre algo que podría considerarse en cierto modo el fenómeno contrario.

La masa de la estrella va disminuyendo principalmente por radiación, y eso afecta a su interacción gravitatoria con cada planeta por separado. Esta redistribución de masa también influye en la relaciones que se producen en la totalidad del sistema. Las naves espaciales van perdiendo masa (de combustible) en su viaje, lo cual incide sensiblemente en su relación, de una parte, con el planeta de partida (también con el resto de cuerpos presentes en el viaje), de otra, con las posibilidades de su propio alcance en el viaje.

La relación entre el tamaño del vehículo y el combustible necesario para garantizar la viabilidad del viaje teniendo en cuenta, además, el instrumental que se pretende transportar es un reto que hay superar.

Optimización de trayectorias

Este problema surge debido a que en las rutas interplanetarias no es posible encontrar “estaciones de servicio” disponibles, y por lo tanto el vehículo espacial necesita llevar consigo de salida la cantidad de combustible que precisa para llevar adelante el viaje previsto, es decir que la nave ha de ser autosuficiente (o como alternativa servirse de fuentes de energía no usuales en nuestros desplazamientos y actividades terrestres).

La duración en buenas condiciones de operatividad de las naves espaciales es un lapso muy breve.

De ahí que haya que encontrar la relación óptima entre la trayectoria, el tiempo invertido y la vida útil del vehículo para diseñar mejor el itinerario del viaje. Hay que tener en cuenta, también, que la duración en buenas condiciones y en plenitud de operatividad de las naves espaciales es un lapso muy breve en comparación con la de los astros; pero eso nos da una ventaja; la de saber que estos últimos, en el corto plazo, tienen la estabilidad de sus trayectorias garantizada [2]; lo que permite decidir la ocasión y el lugar de la toma de contacto de una nave de origen terrestre con determinado cuerpo.

Aquí un inciso para indicar que la noción de optimización del viaje espacial es un poco distinta a nuestra idea habitual de viajes sobre la superficie de la Tierra en la que prevalece, por ejemplo, la necesidad de invertir el menor tiempo posible (disponemos de poco tiempo vital), o minimizar el costo en términos económicos (ahorro energético). Expresado de otra manera, las condiciones principales no son exactamente similares en ambas situaciones. Un caso prototipo está representado por las diferentes modalidades ensayadas para realizar visitas a nuestro vecino más próximo; la Luna [3].

Transferencias orbitales

Así pues, retomando el hilo principal, vemos la necesidad de realizar transferencias eficientes entre órbitas como etapas cruciales en los viajes interplanetarios que parten de la Tierra. Para realizar estos cambios hay que efectuar una secuencia de maniobras orbitales muy precisas. Existen varios procedimientos, los conocimientos teóricos derivan de un trabajo de matemática-física muy complicado y de una tecnología de alto nivel.

El primer procedimiento es el método de Hohmann.

Vamos a ver aquí esbozados, como ejemplo, dos modalidades diferentes de paso entre órbitas circulares. El primer procedimiento es el método de Hohmann -en honor de W. Hohmann (1880-1945) ingeniero estudioso de las órbitas de transferencia en mecánica celeste- y requiere dos maniobras muy bien ajustadas para realizar un cambio desde una trayectoria circular a la siguiente, coplanaria con la primera mediante una elipse de transición interior tangente a ambas, véanse los puntos A y B en (Fig. 3a). Los cambios de velocidades que se precisan se computan teniendo en cuenta una magnitud muy interesante en mecánica celeste; el momento angular.

Mientras que en el segundo (Fig. 3b) lo que se observa es una transferencia bielíptica, es decir que para pasar de una órbita a otra se trazan dos semielipses que cambian el cuerpo del punto A de la primera órbita al punto B de la segunda órbita circular, por la parte exterior de las circunferencias.

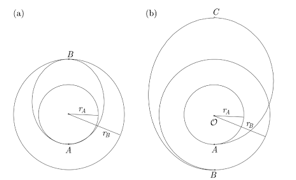
Figura 3. Transferencia de órbitas en naves espaciales

Estas formas de paso de unas órbitas a otras se prueban y se están empleando en misiones espaciales. ¡Bonitos juegos de trayectorias! … y muy útiles.

Referencias

[1] HERRERA, R.M.: “El piano y la Luna” Ciencia y Cultura C2, Monterrey, 2015

[2] HERRERA, R.M.: “¿Por qué la noche es oscura?, C2, Monterrey, 2015

[3] HERRERA, R.M.: Resonancias en el Sistema Solar, Neomenia, Madrid, 2012

[4] HERRERA, R.M.: “Urania y los caminos del cielo” Ciencia y Cultura C2, Monterrey, 2015

[5] MILANI, A. & GRONCHI, C.: Theory of the orbit determination, Cambridge University Press, 2010

[6] MOSER, J.K.: Is the Solar System Stable?, The Mathematical Intelligencer. pp. 65-71, 1978

[7] MOSER, J.K.: Stable and Random Motions in Dynamical Systems, Princenton Landarmarks in Mathematics

[8] POINCARÉ, H.: Les méthodes nouvelles de la mécanique céleste, Gauthier-Villars et fils, 1899 (reprint Dover 1957)

[9] SIEGEL, C.L. & MOSER, J.K. & KALME, Ch.I.: Lectures on Celestial Mechanics, Springer, 1994

Acotaciones

[1] unos 11000 m

[2] Aunque en el largo plazo la estabilidad no está garantizada, sobre todo en los planetas interiores.

[3] Este caso será posiblemente tratado con más detalle en una artículo posterior.

Sobre el autor

Rosa María Herrera

Profesora e Investigadora en UPM, España

Estudió física. Su interés es sobre la estabilidad dinámica del Sistema Solar y los sistemas hamiltonianos de baja dimensión. Se interesa además por los principios variacionales en física y la divulgación científica.