Este artículo se publicó originalmente en la Revista Avance y Perspectiva, Vol. 4 – Núm 2
La Naturaleza es una fuente prácticamente inagotable de patrones geométricos diferentes, como las corrientes de convección que se manifiestan en nubes ordenadas, así como los copos de nieve.
Los patrones son también muy comunes en el mundo vivo, como por ejemplo en la exquisita disposición de las hojas a lo largo del tallo de las plantas o filotaxia, las conchas espirales de algunos caracoles y las pelambres de las cebras y los leopardos. En muchos casos estos patrones tienen un significado funcional para los organismos, proporcionándoles ventajas y capacidad de ejecutar procesos biológicos variados. A este respecto se pueden formular las siguientes preguntas fundamentales: ¿Cómo se forman los patrones naturales? ¿Se pueden describir de forma generalizada los procesos de generación de patrones en sistemas diversos? ¿Cómo pueden describirse estos procesos mediante un modelo matemático?
¿Cómo pueden describirse estos procesos mediante un modelo matemático?
En el año 1917 D’Arcy Wentworth Thompson publicó su magnífico libro On Growth and Form, en el cual demostró que la emergencia de patrones no homogéneos se puede describir mediante procesos físicos y ecuaciones simples. El libro de D’Arcy Thompson sirvió de inspiración para el célebre matemático inglés, Alan Mathison Turing, uno de los padres de la ciencia de la computación. En su clásico artículo The chemical basis of morphogenesis, que se publicó en 1952, dos años antes de su muerte, Turing describió sucintamente, por medio de un sistema de dos ecuaciones diferenciales, un mecanismo posible que puede llevar a la formación de patrones no homogéneos, rompiendo la simetría de translación de un sistema homogéneo.
Según el modelo mínimo de Turing, dos sustancias, a las que él llamó morfógenos, interactúan y se difunden mediante el movimiento browniano causado por los choques con las moléculas del medio o solventes, como demostró Einstein en uno de sus célebres trabajos de 1905, y comprobó experimentalmente Perrin. La difusión generalmente promueve la homogenización espacial de una sustancia: por ejemplo, si añadimos una gota de leche o tinta a un vaso de agua, después de un lapso de tiempo encontraremos las partículas en cualquier parte del vaso. Sin embargo, uno de los aspectos más sorprendentes del mecanismo de Turing es que en ciertas condiciones la difusión puede causar el resultado opuesto; o sea, producir distribuciones espaciales no homogéneas. Para que se formen patrones no homogéneos, el modelo de Turing indica que el primero de los morfógenos debe activar tanto su propia producción como la del segundo. Además, el segundo morfógeno debe inhibir la función del primero. Por lo tanto, llamaremos al primer morfógeno activador, y al segundo, inhibidor. Otra condición necesaria para la emergencia de un patrón no homogéneo es que el coeficiente de difusión del inhibidor sea significantemente mayor que el del activador.
Estas condiciones son muy restrictivas, por lo que durante muchos años impidieron la observación convincente de patrones de Turing; que no se describieron hasta los años 90, casi cuarenta años después de que el mecanismo fuera predicho. Incluso cuando se cumplen dichas condiciones, los patrones aparecen en un rango muy pequeño de los parámetros que aparecen en las ecuaciones de reacción-difusión; de manera que cambios pequeños en estos parámetros puede causar que no se formen los patrones.
El modelo de Turing está basado en dos suposiciones: el determinismo y la conservación de masa.
El modelo de Turing está basado en dos suposiciones: el determinismo y la conservación de masa. Las ecuaciones de reacción-difusión no incluyen de forma explícita ningún término de ruido, y las masas de los morfógenos no cambian con el tiempo. Numerosas investigaciones realizadas en los últimos años muestran que células biológicas que contienen la misma información genética exhiben diferencias significativas en su expresión. Estas diferencias son manifestaciones de variaciones en el número de moléculas en células diferentes, las cuales resultan del carácter estocástico de los procesos de expresión genética. Estas variaciones son conocidas como ruido demográfico. Cabe preguntarse cómo en un organismo multicelular el ruido demográfico entre diferentes células influye la creación de patrones precisos, y cómo en el modelo de Turing la emergencia de patrones puede verse influida al descartar la suposición de equilibrio e incluir el ruido demográfico.
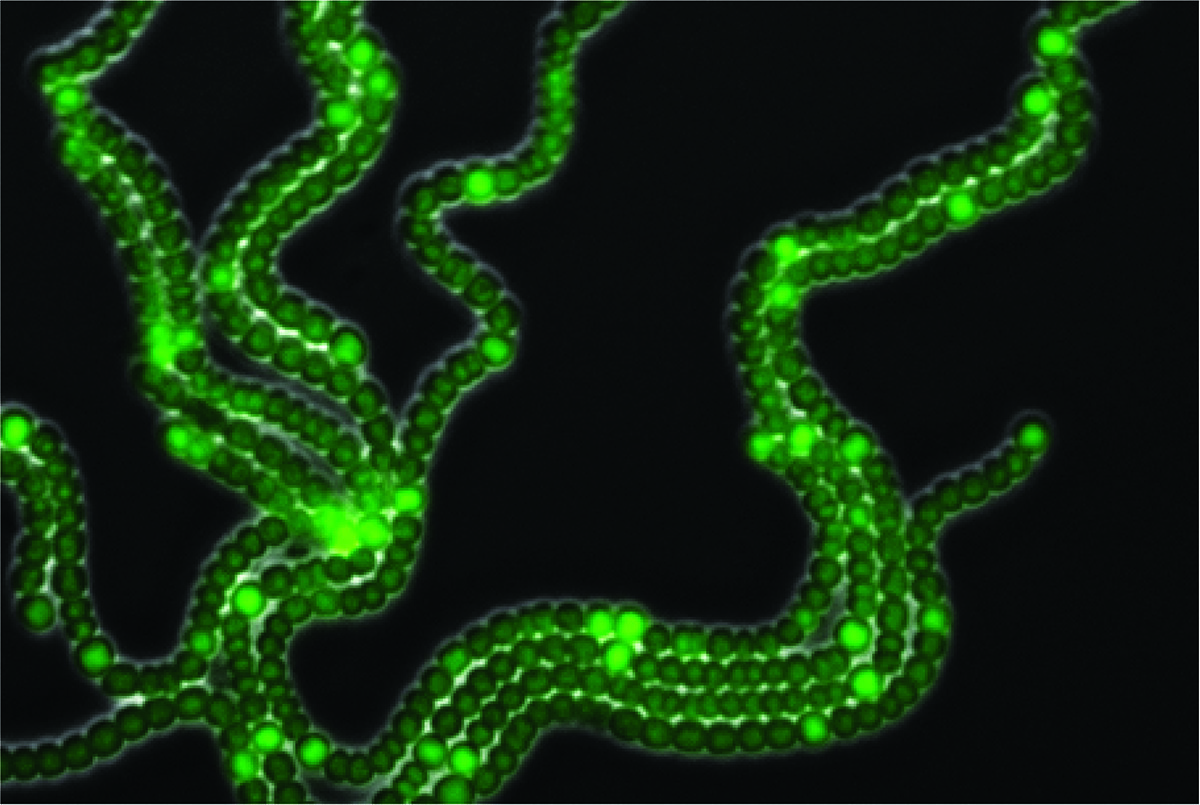
Anabaena, un organismo multicelular perteneciente al grupo de las cianobacterias, es un modelo elegante y simple que permite estudiar preguntas fundamentales sobre la emergencia de patrones biológicos. Millones de años antes de que las primeras plantas aparecieran sobre la Tierra, las cianobacterias enriquecieron la atmósfera primitiva con oxígeno mediante el proceso de fotosíntesis, y comenzaron a fijar el nitrógeno necesario para la existencia de plantas y animales. Anabaena es una cianobacteria filamentosa que presenta procesos de desarrollo, y la diferenciación de algunas de sus células puede seguirse a nivel de células individuales. Otra gran ventaja de este modelo biológico es que como máximo sólo presenta dos tipos de células, mientras que la mosca Drosophila tiene más o menos 60 tipos, y Homo sapiens 250. En el filamento de Anabaena cada célula tiene dos vecinas, con las cuales mantiene comunicación, una a su izquierda y otra a su derecha. En condiciones ambientales de abundancia de nutrientes, todas las células llevan a cabo la fotosíntesis oxigénica y utilizan como fuente de nitrógeno compuestos fácilmente asimilables como el amonio y el nitrato, que utilizan para la producción de proteínas. Cuando el organismo está expuesto a condiciones de escasez de nitrógeno, algunas de sus células se diferencian en heterocistos, células especializadas en la fijación de nitrógeno atmosférico.
En el filamento de Anabaena cada célula tiene dos vecinas…
La fijación del nitrógeno está mediada por una enzima especializada, la nitrogenasa, que se inactiva por cantidades casi indetectables de oxígeno. De esta forma podría decirse que la fijación de nitrógeno (extremadamente sensible al oxígeno) y la fotosíntesis (que conlleva la producción de oxígeno) constituyen dos procesos incompatibles. La formación de heterocistos resuelve la incompatibilidad entre estos dos procesos, resultando en la división de tareas entre las distintas células del filamento: las células que no se diferencian continúan llevando a cabo la fotosíntesis, proporcionando carbohidratos y energía a los heterocistos, mientras que estos últimos surten a las células vegetativas con una fuente de nitrógeno utilizable. De esta forma emerge uno de los patrones más simples en la Naturaleza consistente en una sucesión de heterocistos individuales separados por intervalos de 10-15 células vegetativas. Numerosos trabajos llevados a cabo por microbiólogos durante las últimas décadas han mostrado que los patrones en Anabaena se forman mediante la actividad de genes cuyos productos actúan como activadores e inhibidores, precisamente como predice el modelo abstracto de Turing. Además, los morfógenos inhibidores pueden pasar de célula a célula a lo largo de un filamento. Otros estudios también han mostrado que en Anabaena el ruido demográfico es significativo y que, sin duda, influye en las decisiones celulares de diferenciación.
En efecto, un modelo reciente de formación de patrones en Anabaena en el que el ruido demográfico juega un papel preponderante ha demostrado que dicho ruido puede fomentar la formación de patrones transitorios en rangos de parámetros que no permiten la formación de patrones deterministas, o sea en regiones en las que el sistema determinista es homogéneo. Por lo tanto, estos llamados patrones estocásticos de Turing se forman en rangos de parámetros mucho más amplios que los de los patrones deterministas. Posteriormente, estos patrones estocásticos pueden ser fijados por otros procesos, resultando así en los patrones que vemos en la Naturaleza.
La inclusión de ruido en el modelo de Turing podría explicar la formación de patrones en otros sistemas biológicos, en los que los modelos deterministas predicen que sólo se podrían formar patrones en condiciones muy limitadas. Como ejemplos de estos sistemas pueden citarse la formación de biopelículas bacterianas sintéticas, los patrones de la epidermis de hojas y raíces en plantas y diversos sistemas ecológicos.
En sistemas complejos, el ruido es un factor nocivo en varios casos.
En sistemas complejos, el ruido es un factor nocivo en varios casos. De hecho, es común pensar que durante procesos de desarrollo y diferenciación el ruido puede inducir a una célula a tomar una decisión errónea y seguir un destino equivocado. Por ello muchos científicos han sido de la opinión de que el ruido debe de ser filtrado. Sin embargo, los últimos resultados proporcionan evidencias crecientes de que, al menos en varias circunstancias, el ruido no es un factor negativo, sino un componente necesario para el funcionamiento correcto de los sistemas biológicos.
Un modelo determinista deja de lado la suposición de que los procesos naturales están influidos por el azar y el ruido. Esta suposición es válida en algunos casos, como en el movimiento de los planetas alrededor del sol, tal como entendieron Copérnico y Newton. Sin embargo, los avances científicos han conducido al entendimiento de que el gran número de partículas que constituyen la materia, junto con la incapacidad de describirlas todas, resultan en procesos de carácter estocástico. Estos procesos forman parte integral y necesaria de varios sistemas naturales en general, y de los seres vivos en particular. Por lo tanto, no es sorprendente que a lo largo de la evolución diversos mecanismos hayan aprovechado el ruido incluso para formar patrones de desarrollo.
El lector interesado puede ahondar en el tema aquí: https://doi.org/10.3390/life8040058