Hace tiempo vivíamos junto a una calle bastante transitada y la recámara de mi hija era muy ruidosa, así que decidí instalarle una ventana aislante que vi anunciada en el periódico. El proveedor tenía una página en la internet donde informaba detalladamente sobre su construcción: consistía en dos paneles de vidrio paralelos, separados entre sí por un marco de aluminio, al que se encontraban unidos herméticamente, con un vacío parcial en la cavidad intermedia. La publicidad prometía una reducción del ruido a la mitad. No fue barata, pero hice el gasto con la ilusión de que mi hija tuviera noches más apacibles. Una vez instalada, la diferencia acústica con la anterior me resultó imperceptible. La recámara seguía tan ruidosa como antes, pero ahora con una ventana cara. La experiencia prometía ser frustrante, pero resultó tan aleccionadora que ahora me gusta contarla, pues es mucho lo que he aprendido de ella.
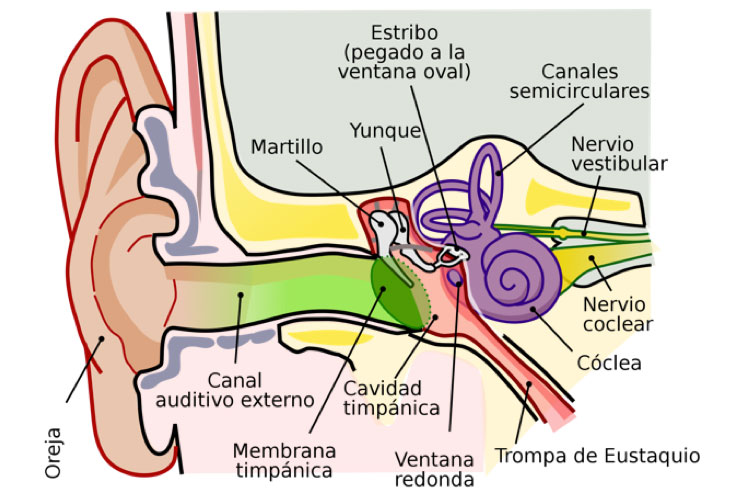
Nuestros oídos están llenos de sorpresas. Su parte externa, las orejas, nunca dejan de crecer y ayudan tanto a detectar con precisión asombrosa la dirección de procedencia de un sonido, como a darnos una buena idea de la distancia a la que se origina. Sus principales funciones ocurren dentro de la cabeza, donde los oídos parecen tener magia por poco más que tres huesos diminutos de nombres con resonancias medievales, martillo, yunque y estribo, “unas briznas de músculos y ligamentos, una delicada membrana y un puñado de células nerviosas.”[1] Mi abuela solía decir, desde su muy particular punto de vista y con el aplome bondadoso y juicioso ganado a lo largo de muchos años bien vividos, que los oídos eran como el cofre de un tesoro pirata, colmado de joyas propias y ajenas. La historia de la ventana me permitió corroborar una vez más cuánta razón tenía.
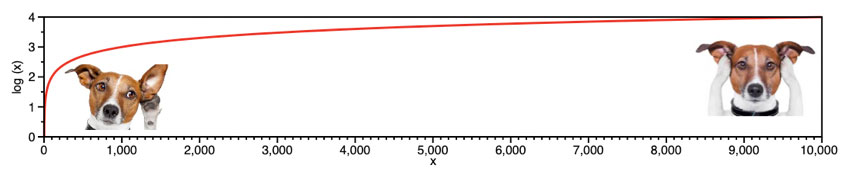
Los oídos pueden detectar diferencias de presiones en el aire de veinte micro pascales,[2] casi cien veces menores que la ejercida por un diminuto plumón de polluelo sobre la palma de la mano. Una vez cruzado dicho nivel mínimo de sensibilidad, o umbral de audición,[3] el oído sigue detectando sonidos hasta alcanzar el umbral de dolor, cuando su fuerza es un millón de millones de veces mayor.[4] Nuestros oídos pueden lograr semejantes proezas porque su reacción amplifica los ruidos leves y atenúa los fuertes. Entre las funciones matemáticas sencillas, el logaritmo es la que mejor describe la forma en que el oído reacciona a la intensidad acústica.[5] Por este motivo se usa una escala logarítmica para medir el volumen de los ruidos: una amplitud de un bel (representado por el símbolo B), equivalente a 10 decibeles (representados por el símbolo dB), implica un sonido diez veces más potente que el límite mínimo de audición; 2 B una amplitud cien veces mayor; el umbral de dolor se alcanza a los 120 dB.[6] El ruido de una calle muy transitada, como la que colindaba con la recámara de mi hija, ronda los 90 dB, por lo que a una disminución de su intensidad a la mitad le corresponde una caía del 3.3% en escala logarítmica, equivalente a unos 3 dB. Es probable que hubiera podido notarla, de haber sido posible alternar las ventanas repetidamente para contrastarlas al instante, pero transcurridas las horas que tomó la remoción de la ventana anterior y la instalación de la nueva, en un contexto de expectativas muy altas, me resultó imposible detectar la diferencia a oreja pelada. La persona que me vendió la ventana me engañó con la verdad.
Uno se pregunta entonces, ¿de qué tamaño debería haber sido la reducción del ruido para que se notara? Según las fuentes que consulté en la internet, el umbral diferencial es de unos 0.4 dB, aunque yo lo consideraría unas diez veces mayor en condiciones descontroladas, a juzgar por mi experiencia con la ventana.[7] Esos 0.4 dB corresponden a una variación aproximada del 10% en la intensidad del sonido. Este dato es relevante porque los sensores logarítmicos tienen la particularidad de reaccionar a estímulos proporcionales al ruido en el que se encuentran inmersos.[8] Si la proporción es del 10%, como parece ser el caso en condiciones controladas en el laboratorio, entonces se necesita un incremento de escasas 10 veces el umbral de audición para que un aumento en el volumen sea perceptible dentro de una biblioteca, donde el ruido ambiental es de unos 20 dB. En cambio, en una calle transitada, como la que perturbaba el sueño de mi hija, la disminución perceptible es de cien millones de veces la intensidad de dicho umbral. A esto me refería con anterioridad al decir que nuestros oídos amplifican los ruidos leves y atenúan los fuertes, aunque tal vez sea mejor señalar que son mucho más sensibles a los sonidos leves que a los fuertes.
No puedo dejar de preguntarme cuáles serán las ventajas y desventajas de todo esto, más allá del gasto inútil que hice al comprar la ventana. Intuyo que la atenuación logarítmica ayuda a evitar la destrucción de nuestros oídos en las condiciones actuales de ruido ambiental, aunque también cuenten con el reflejo auricular: un mecanismo de protección que separa momentáneamente al estribo de la cóclea ante aumentos súbitos en la intensidad de los ruidos por arriba del umbral de dolor y que funciona mientras los cambios no sean muy rápidos ni permanentes. En un estadio de futbol, por decir algo, pueden alcanzarse 140 dB durante una buena jugada de gol, por lo que no es raro experimentar un poco de sordera posterior, mientras el estribo regresa a su lugar. Sin embargo, estas condiciones son recientes y no influyeron en el desarrollo evolutivo de nuestros oídos, lo cual es muy probable que haya ocurrido en ambientes más bien silenciosos. Así es como imagino a Lucy, la australopithecus afarensis más famosa del mundo, caminando con sigilo entre matorrales silentes, capaz de detectar el menor de los ruidos, presentir fauces enormes y salir corriendo despavorida hasta llegar a casa para contarlo. Algunos de sus congéneres habrán reaccionado con mayor parsimonia, pero seguramente el tiempo los expulsó de la competencia evolutiva, con ayuda de leopardos hambrientos, heredándonos el instinto anacrónico de asustarnos con cualquier murmullo, sobre todo si estamos en lugares oscuros y poco familiares. En todo caso, como haya sido, la mayor sensibilidad a los ruidos leves parece haber constituido una ventaja evolutiva relevante. ¿O habrá sido lo asustadizo? ¿O ambas cosas?

Estando sobre esta ruta de ideas, uno se pregunta si acaso poseemos otros sentidos con características similares. La respuesta que encontré es muy interesante. Resulta que sí. De hecho, esa es la regla y hasta tiene nombre: Ley de Weber-Fechner.[9] Esta ley, formulada en la segunda mitad del siglo XIX, establece que “si la intensidad de un estímulo crece en progresión geométrica, su percepción lo hará en progresión aritmética.” Es decir, si la intensidad de un estímulo aumenta como 10x, su percepción experimenta un incremento de x, como ocurre con la audición. En otras palabras, la magnitud de la percepción varía como el logaritmo de la intensidad del estímulo. O, si se quiere, los cambios perceptibles en la intensidad de un estímulo son proporcionales a la intensidad del estímulo.[10] En palabras de la Wikipedia:[11]
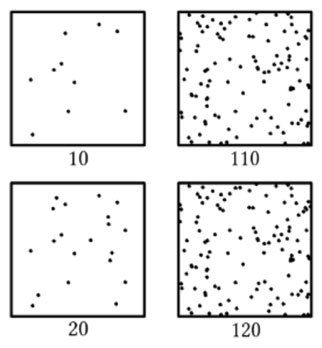
“Si estamos sosteniendo en nuestra mano una masa de 100 gramos, tal vez no la podamos distinguir de otra de 105 gramos, pero sí de una de 110 gramos. En este caso, el umbral para discernir el cambio de masa es de 10 gramos. Pero en el caso de sostener una masa de 1000 gramos, 10 gramos no serán suficientes para que notemos la diferencia, al ser el umbral proporcional a la magnitud del estímulo. En su lugar, nos hará falta añadir 100 gramos para notar la diferencia. Dicho de otro modo, nuestra capacidad de apreciación ante un cambio se basa en «el valor relativo de la variación respecto del valor de partida». Se puede expresar en porcentaje aproximado, que es totalmente subjetivo dependiendo de la sensibilidad de cada individuo. La percepción puede referirse, generalmente, a estímulos sensoriales primitivos como la luz, el ruido, el olor, etc., o compuestos (que se derivan al combinarse en un sexto sentido algunos de los anteriores), como el peso, la velocidad, una vibración, la presión, el calor, un dolor, un golpe, un mareo, etc.”
El rango de validez de la ley de Weber-Fechner es tan amplio que incluye la percepción del tiempo. Por eso en la niñez un día puede parecer eterno y en la vejez un año llega a ser efímero. Incluso nuestra forma de pensar sobre los aspectos sociales más complejos suele ser logarítmica.[12]
Siguiendo con la idea de que la evolución pudo haber favorecido el desarrollo de sentidos logarítmicos, surge la pregunta de si los hubo de otro tipo, antes de que los primeros prevalecieran, o si aún los hay. Al parecer, desde que los primeros organismos pluricelulares anexaron algunas células fotosensibles a sus cuerpos, los ojos han evolucionado independientemente por lo menos unas cuarenta veces.[13] Otro tanto parece haber ocurrido con los oídos,[14] aunque no tengo idea de si todos responden de forma logarítmica a los estímulos. No he pensado sobre cómo poner a prueba la ley de Weber-Fechner en otras especies, pero tengo la impresión de que la gran mayoría de los bichos, con los que me he topado en condiciones normales, tienen reacciones básicas muy parecidas a las mías, ya sean mamíferos, aves, reptiles, peces, insectos, arácnidos, moluscos, crustáceos, etcétera. Esa aparente generalidad despierta la duda de si la respuesta logarítmica no estará más bien ligada a alguna ley física que, por lo mismo, se cumple siempre. En ese caso la ventaja evolutiva no vendría de aprovechar dicha ley, que pondría el piso parejo para todas las especies, sino de la habilidad de poder escapar a tiempo de los depredadores, reales o imaginarios, que es mayor en las especies asustadizas.
Prosiguiendo con la búsqueda de la raíz del misterioso logaritmo que portamos entre las orejas, cuya incomprensión me llevó a caer en el fiasco de la ventana, la posibilidad de que su origen no sea biológico lleva a buscar objetos inanimados que respondan de forma logarítmica cuando se les perturba. Lo primero que me viene a la mente son los efectos que los movimientos telúricos tienen sobre la infraestructura citadina moderna. Pasando por alto detalles técnicos y hablando de forma burda, la intensidad de los temblores se mide precisamente en escala logarítmica, porque se requiere un temblor mil veces más fuerte para provocar tres veces más daño.[15] Sin embargo, los edificios y puentes son las manifestaciones materiales de las ideas plasmadas en los planos de construcción. Ideas que han ido replicándose y mutando con el tiempo, sujetas a la selección natural que permite sobrevivir a aquellas que producen edificios y puentes más estables. Y la mejor manera de resistir al embate de la naturaleza, cuando ésta decide mostrar sus músculos, es reaccionando logarítmicamente.
Algunos científicos piensan que hay dos tipos de vida en el mundo: la genética y la memética.[16] En el primero, los seres vivos serían los genes y las especies biológicas su manifestación material, o fenotipo. En el segundo, las ideas serían los seres vivos y su expresión material la realización de dichas ideas, como los edificios y puentes, o un delicioso platillo navideño codificado en su receta. Se basan en que ambas cosas, genes e ideas, parecen cumplir con los principios del darwinismo universal, en el sentido de que son entes mutantes, replicables de forma espontánea y sujetos a selección natural. Al parecer, eso es todo lo que se necesita para que algo esté vivo. De ser así, la respuesta logarítmica de la infraestructura citadina moderna a los temblores podría ser el resultado de la evolución de las ideas, lo que nos regresaría a la hipótesis inicial, en el sentido de que los sensores logarítmicos podrían haber sido favorecidos por la evolución.
Sin embargo, la aparente generalidad de las percepciones logarítmicas no disminuye con lo anterior, sino que se acrecienta. Por lo mismo, la idea de que su origen sea alguna ley física resulta aún más atractiva que antes. Tal vez esa sea la única forma en que pueden reaccionar las estructuras complejas, codificadas en genes o memes, o de cualquier otra naturaleza, incluso sin intervención de la vida. Tal vez el éxito evolutivo radica en generar complejidad, para que las reacciones sean logarítmicas. Mas, si ese fuera el caso, ¿cuánta complejidad se requiere para que ocurra? ¿Cómo se mide la complejidad?[17] Tampoco podemos descartar la posibilidad de que sea algo que también ocurre con las estructuras simples. Sólo se necesita que las percepciones estén ligadas a alguna variable que se sume cuando los estímulos se multipliquen, algo que sólo puede lograrse a través de una dependencia logarítmica.[18] Es decir, una variable cuyo valor crezca en progresión aritmética cuando el estímulo lo haga en progresión geométrica.
La entropía cambia logarítmicamente con la dispersión de las variables moleculares de los materiales,[19] la cual suele aumentar geométricamente con la energía. En el caso de los gases diluidos, como el aire que transmite las ondas sonoras, este comportamiento se convierte en una dependencia logarítmica de la presión, pero no tengo idea de cómo relacionar este hecho con el comportamiento fisiológico de los oídos. No hay, por otro lado, una relación similar entre la entropía y la intensidad de un haz de luz, mas la respuesta de los ojos también es logarítmica. Ni hablar de los sentidos compuestos, como el que permite percibir el transcurrir del tiempo. No tengo ni la menor idea de cómo relacionar una cosa con la otra, pero la entropía es la única variable física que distingue entre pasado, presente y futuro en las condiciones en que escucho música.
Por mucho que me gustaría poder decir que la ventana resultó ser engañosamente entrópica, la verdad es que tengo más dudas que al principio. Nunca pretendí que mi relato llegara a este punto, sino que es hasta aquí que me trajo la ventana y, a decir verdad, espero que me lleve un poco más lejos. Ya les contaré, si eso ocurre. Teniendo en cuenta los efectos secundarios, la compra de la ventana no parece haber sido tan mala, aunque sólo me ha dejado certeza de una cosa: Soy un tipo logarítmico y eso es bastante cool. C2
Notas al pie
[1] Para una lectura tan divertida como interesante de éste y de muchos otros temas recomiendo el libro “El cuerpo humano. Guía para ocupantes” de Bill Bryson (RBA Libros, 2020).
[2] El Pascal (representado por el símbolo Pa) es una unidad de presión más o menos equivalente a la décima parte de la que ejerce un peso de un kilogramo, distribuido sobre una superficie de un metro cuadrado (o una décima de gramo sobre un centímetro cuadrado). Un micro Pascal (representado por el símbolo μPa) es la millonésima parte de un Pa. Una onda sonora que implique diferencias de presión de unos 20 μPa, a frecuencias de unos 2000 Hz, transmite un flujo de energía de unos 10-12 Watts por metro cuadrado, es decir, 0.000000000001 W/m2.
[3] En términos de potencia, el umbral de audición es de 10-12 W/m2. La intensidad de un sonido se mide con relación a este umbral. Por ejemplo, un volumen de 10 decibeles significa una intensidad 10 veces mayor; de 20 decibeles es 100 veces más intenso.
[4] El umbral de dolor se alcanza cuando el flujo de energía es del orden de 1 W/m2. Esto equivale a 120 decibeles. Un sonido de 150 decibeles puede reventar los tímpanos.
[5] La función logaritmo base 10 se define como log(10x)=x. Es decir, si la cantidad 10x aumenta de 10 a 1000, su logaritmo base 10 sólo va de 1 a 3.
[6] El bel recibe su nombre en honor a Alexander Graham Bell y no representa una magnitud física, como lo hacen el metro o el segundo, sino tan sólo la forma en que nos gusta llamar a la manera en que medimos la intensidad de los sonidos. En español suele llamársele belio y a su décima parte decibelio, aunque cada vez cae más en desuso la costumbre de españolizar los nombres de unidades inspiradas en el apellido de personajes ilustres, pues los apellidos no se traducen.
[7] Este valor, como todos los demás que proporciono, es un promedio que en realidad depende de la frecuencia y de la intensidad de los sonidos, así como de otras variables como la edad y el género de los escuchas. Para obtener información más detallada de este y otros aspectos de la audición, recomiendo hacer una búsqueda en la Wikipedia bajo términos como “espectro audible” o “umbral de audición”.
[8] A un sonido de intensidad x veces mayor que el umbral de audición le corresponde la magnitud log(x) en escala logarítmica. Si la intensidad aumenta a x + Δx, su magnitud logarítmica lo hace a log(x + Δx). El cambio en la intensidad es Δx y el correspondiente cambio en su magnitud logarítmica es log(x + Δx) – log(x) = log(1 + Δx/x). De este resultado, que se obtiene utilizando algunas propiedades de las funciones logarítmicas que no se explican en este artículo, puede observarse que los cambios en las magnitudes logarítmicas sólo dependen de la proporción del cambio Δx relativo a la intensidad del ruido ambiente x. Es decir, sólo dependen de Δx/x. En otras palabras, si un sensor responde a estímulos proporcionales al ruido en el que se encuentra inmerso, es evidencia de que se trata de un sensor logarítmico.
[9] Esta ley estableció el inicio de la psicofísica experimental.
[10] Si el cambio en el estímulo percibido, ΔE, es proporcional al cambio en la intensidad del estímulo, ΔI, en relación a la intensidad inicial, I, es decir ΔE = c ΔI/ I, entonces la magnitud del estímulo percibido es E = c log(I) + E0. Aquí, c y E0 son constantes de proporcionalidad y de integración, respectivamente. Debido a que en el umbral, I0 , no hay percepción, entonces E0 = –c log(I0) y, por lo mismo, E = c log(I/I0). La constante de proporcionalidad puede cifrarse arbitrariamente en 1 para la escala logarítmica base 10, con lo que recuperamos la escala acústica, pero en un contexto mucho más amplio.
[11] En la actualidad, la internet es con mucho la fuente de información dominante, pero es muy poco confiable. Por eso, una parte del trabajo de los especialistas debe ser filtrar su contenido en beneficio de sus lectores. Es en este entendido que me atrevo a reproducir párrafos completos de la Wikipedia. Desde luego, citando claramente la fuente. Al final de cuentas, el destino de este artículo también será la internet y, con un poco de suerte, partes de él serán reproducidas y citadas por alguno de sus lectores.
[12] La liga que pongo a continuación lleva a un video de Hannah Fry, donde diserta sobre la ley de Weber en el contexto de algunos de los ejemplos discutidos en este artículo, pero hacia el final también lo hace sobre algunas consecuencias del pensamiento logarítmico en mercadotecnia y en la impartición de justicia. Espero que les resulte tan interesante como a mí: https://www.youtube.com/watch?v=hHG8io5qIU8.
[13] “Evolución de los ojos y fotorreceptores” de M. E. Guido y P. Panzetta (Oftalmología Clínica y Experimental 2007, 1: 26-31). “Evolution of the vertebrate eye: opsins, photoreceptors, retina and eye cup” de T. D. Lamb, S. P. Collin y E. N Pugh (Nat Rev Neurosci. 2007, 8(12): 960-976, DOI: 10.1038/nrn2283). “El relojero ciego” de Richard Dawkins (Tusquets Editores S.A., 2015). “Evolución. El mayor espectáculo sobre la tierra” de Richard Dawkins (Espasa, 2010).
[14] “El origen del oído” de Sarah Lewin (Investigación y Ciencia, julio 2015). “Developmental genetic bases behind the independent origin of the tympanic membrane in mammals and diapsids” de T. Kitazawa et.al. (Nature Communications 2014, 6:6853, DOI: 10.1038/ncomms7853).
[15] Las escalas para medir los efectos de los sismos se desarrollaron hace relativamente poco tiempo. La escala de Richter data de 1935 y corresponde, más o menos, a una escala logarítmica base 30. La escala de Mercalli se propuso a finales del siglo antepasado, pero ha sido revisada muchas veces (una de las revisiones más recientes la hizo el mismo Richter, en 1931). Ella corresponde, aproximadamente, a una escala logarítmica base 10. Ambas tienen dificultades para determinar sus límites de validez, sus umbrales de sensibilidad e incluso los objetos a usarse como sensores, pues los edificios no sienten los temblores débiles. A pesar de todo, son muy útiles para cuantificar la magnitud de los movimientos telúricos y tomar medidas de prevención y auxilio a las poblaciones afectadas por algún evento sísmico. También hay otras escalas más recientes en uso, cada una con sus ventajas y desventajas, pero todas logarítmicas.
[16] “The selfish gene” de Richard Dawkins (4ª edición, OUP Oxford, 2016). “The meme machine” de Susan Blackmore (OUP Oxford, 2000).
[17] El premio Nobel de Física de este año (2021) fue otorgado a S. Manabe y K. Hasselmann por un modelado físico del clima terrestre capaz de cuantificar su variabilidad y de hacer predicciones precisas del calentamiento global. También lo recibió G. Parisi por el descubrimiento de la interrelación entre desorden y fluctuaciones en sistemas físicos, desde escala atómica hasta planetaria. El factor común entre las aportaciones de los galardonados fueron sus contribuciones revolucionarias a la comprensión de sistemas complejos. La naturaleza de la complejidad apenas empieza a comprenderse y es muy probable que defina el perfil de los grandes avances científicos y tecnológicos del siglo XXI.
[18] El logaritmo de un producto es la suma de los logaritmos de los factores: log(ab) = log(a) + log(b).
[19] Me refiero a los valores de las velocidades y posiciones que pueden tomar las moléculas que componen el material o, en su defecto, a los estados cuánticos colectivos que pueden ocupar.


