Hace apenas cuatro días se dio una noticia que, desde el punto de vista del impacto para el conocimiento de nuestro universo, difícilmente encontrará rival en lo que queda del año que recién empieza.
El experimento aLIGO (advanced Laser Interferometer Gravitational-Wave Observatory) confirma que en septiembre del año pasado se observaron ondas gravitacionales producidas por la coalescencia de dos hoyos negros.
Hace poco menos de un siglo, Albert Einstein publicó las ecuaciones de la Teoría General de la Relatividad que explicaban la gravitación universal. En ese mismo año, mientras se enfermaba mortalmente en el frente ruso durante la Primera Guerra Mundial, otro alemán, Karl Schwarzschild, encontró la primera solución a esas ecuaciones. Esta solución describe un objeto muy exótico: un hoyo negro. Unos meses después, Einstein haría otra predicción fundamental de su teoría: las ondas gravitacionales. Para entender de qué estoy hablando, véanse las figuras 1-3. Corresponden a una misma bola de acero cayendo en tres líquidos diferentes: agua (figura 1), aceite (figura 2) y glicerina (figura 3). Sabemos que mientras más viscoso es el líquido, más lentamente cae la bola. Además, también podemos distinguir entre cada caso prestando atención a las diferencias entre las estelas que la bola de acero deja detrás al caer en el líquido.



Imaginemos que la única información que tenemos es la que podemos observar en las paredes de la probeta, en los puntos donde están los conos. O sea, no vemos nada de lo que sucede en el interior. Parece poco, pero no lo es. En primer lugar, obviamente podemos decir si algo está cayendo dentro del líquido o no por la estela que nos llega. Hay dos detalles adicionales importantes. El primero es que podemos verificar si realmente algo está cayendo, porque la información obtenida en el primer punto puede confirmarse con lo que observemos en el segundo; el otro detalle es que recibimos la información después de que el objeto pasó el punto donde estamos observando. Existe una ley física, llamada ley de Stokes, que nos permite describir la caída de una esfera en un líquido y esa descripción depende del radio de la esfera y la viscosidad del líquido. Midiendo el tiempo que transcurre entre que recibimos la información en el primer punto y luego en el segundo punto, podemos estimar la velocidad de la caída y, usando la ley de Stokes, determinar el tamaño de la esfera y en qué tipo de líquido está cayendo. Por último, si tenemos previamente un catálogo de patrones de las estelas de diferentes líquidos perturbados por diferentes tipos de esferas (plásticas, de acero, sólidas, huecas, etc), sacando fotos de las estelas al llegar a las paredes de la probeta podemos determinar a cuál patrón se asemeja más y tener una idea bastante precisa sobre lo que sucedió dentro del líquido y cuándo sucedió.
A mayor “viscosidad” del “líquido”, más lenta la caída.
Una de las predicciones inmediatas de la Teoría General de la Relatividad es que el espacio, el escenario donde realizamos todas nuestras actividades, el escenario donde tiene lugar todo lo que sucede en nuestro universo, es como ese líquido. No es el escenario inmutable de un teatro con los artistas moviéndose en él sin alterarlo, es un medio que reacciona a nuestra presencia y condiciona cómo podemos movernos. A mayor “viscosidad” del “líquido”, más lenta la caída; entre más grande el objeto que cae, mayor la perturbación que provoca en el “líquido”. Aún más, no sólo el espacio, sino también el tiempo se ve afectado por la existencia de los objetos que caen y, a su vez, afecta cómo caen estos objetos. O sea, las mediciones de un reloj en un “líquido” con cierta “viscosidad” o “cayendo” junto a una “esfera” de cierto tamaño, serán diferentes a las de un reloj en un “líquido” con otra “viscosidad” o en reposo con respecto a un punto en las “paredes” de la “probeta”. La analogía correcta sería que el líquido es como el espacio-tiempo y la materia es como la esfera que está cayendo. En el Universo tenemos diferentes tipos de materia en diferentes condiciones, por lo que la analogía para todo el Universo sería la de un líquido con diferentes viscosidades en diferentes regiones y esferas de diferentes tipos y de diferentes radios cayendo en él. Dependiendo del tamaño y el tipo de la esfera y de la viscosidad de la región en que se está moviendo será el patrón de las perturbaciones que se transmitirán al resto del líquido. Las perturbaciones del espacio-tiempo son las que nos traen la información sobre los cambios en su estructura. Éstas son las ondas gravitacionales. Y tal como sucede con la estela en el líquido, la información sobre el cambio del espacio-tiempo en un cierto lugar se demora cierto lapso de tiempo en transmitirse a otras partes del Universo. Como el Universo es tan grande, ese lapso puede ser de miles de millones de años por lo que, para percibirla, la perturbación debe ser gigantesca, por ejemplo, la explosión de una supernova.
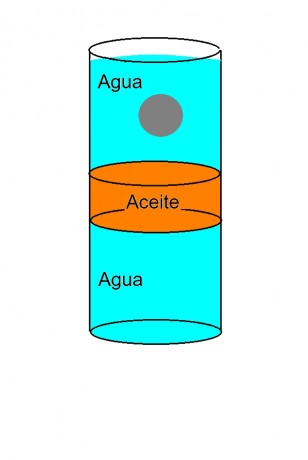
Por otra parte, imaginemos ahora que tenemos una probeta con agua y una capa de aceite justo en el medio, como se muestra en la figura 4. Al caer por el agua que está arriba, una determinada esfera adquirirá cierta velocidad y al entrar al aceite (que es más viscoso) se verá frenada. Al atravesar esa capa intermedia, volverá a acelerarse a medida que siga cayendo en el agua. Supongamos que en vez de aceite usamos otro líquido más viscoso en la capa intermedia. Entonces será mayor la desaceleración (el frenado) que sufrirá la esfera al entrar a ese líquido. Siguiendo con esta línea de razonamiento, no es difícil imaginar que con un líquido suficientemente viscoso, la esfera será completamente frenada y su caída se detendrá, sin llegar nunca a la siguiente capa de agua. Para terminar, imaginemos que existe un líquido tan viscoso que ninguna esfera sería capaz de atravesarlo, sin importar su radio, su tipo o la velocidad con la que entre a la capa más viscosa. Esta es la analogía para la solución de Schwarzschild: describe una región del espacio-tiempo tan “viscosa” que nada puede atravesarla. Cuando digo nada, incluyo a la luz, por lo que entonces, nunca nos llegará luz desde dentro de esa región. Así que observando todo el espacio-tiempo a su alrededor, con sus estrellas y otros objetos brillantes, al pasar nuestra vista por esta región tan “viscosa” veremos, como contraste, una esfera oscura, que es a lo que luego se le dio el nombre de hoyo negro. Los hoyos negros son una solución matemática a las ecuaciones de Einstein y, como tal, no es obligatorio que existan en la realidad (las matemáticas permiten universos incompatibles con las observaciones). No obstante, desde su predicción han sido objeto de búsqueda por los astrónomos. Su naturaleza hace imposible observarlos directamente, pero se puede intentar detectar las consecuencias de su existencia. Hasta hoy, existen varios objetos astrofísicos que, si no son hoyos negros, es muy difícil explicar qué son. Sin embargo, que sea difícil no excluye completamente la posibilidad de que sean otro tipo de objetos exóticos extraordinariamente compactos. Y para los científicos, gente esencialmente escéptica, es crucial la certidumbre.
[blockquote author=”” pull=”pullleftt”]Es relevante tomar en cuenta que la mayoría de los criterios se usan para determinar si lo observado es un hoyo negro o no.
Es relevante tomar en cuenta que la mayoría de los criterios que se usan para determinar si lo observado es un hoyo negro o no, se fundamentan en conceptos físicos que tienen que ver con la Teoría General de la Relatividad. La observación de un efecto predicho como solución de las ecuaciones de Einstein sería más concluyente. El problema es que cuando se quieren describir fenómenos reales, estas ecuaciones se vuelven extraordinariamente difíciles de resolver de la forma que lo hizo Schwarzschild hace 100 años. Pero estamos en el siglo XXI, y desde hace años usamos las computadoras cada vez que las ecuaciones parecen insolubles. El uso de estas herramientas para resolver las ecuaciones de Einstein es una rama de la Física que se conoce como Relatividad Numérica. Gracias a los códigos implementados por los investigadores de esta área (varios de los cuales trabajan en instituciones mexicanas) se ha podido establecer un catálogo de patrones de ondas gravitacionales producidas por diferentes fenómenos astrofísicos, entre ellos, la formación de un hoyo negro como fase final del colapso de una supernova.
¿Cómo se pueden detectar las ondas gravitacionales?
Lo que necesitamos es detectar las ondas gravitacionales producidas por cualquier proceso relacionado con un hoyo negro. Desde mediados del siglo pasado los científicos se propusieron detectar las ondas gravitacionales, o sea, perturbaciones del espacio-tiempo. ¿Cómo se pueden detectar? Lo más sencillo, un cambio de distancia entre objetos perfectamente inmóviles cada uno con respecto al otro. Si volvemos a ver las figuras de las bolas cayendo en el líquido, no es difícil comprender que mientras no pasa la bola, la distancia entre cualesquiera dos puntos en el líquido permanece prácticamente invariante, pero al pasar la bola, deja atrás la estela que agita el líquido y por momentos acerca a esos puntos y por momentos los aleja. Recordando que el líquido es como el espacio-tiempo, tenemos que durante el paso de una onda gravitacional, la distancia entre dos puntos del espacio oscila. El gigantesco detalle es que, para la mayoría de los fenómenos astrofísicos, esa distancia resulta ser insignificante, mucho más insignificante que lo que nosotros podamos creer.
Y aquí entra el experimento aLIGO. Éste se encuentra en dos observatorios, uno en Livingston (Louisiana) y otro en Hanford (estado de Washington), separados por una distancia de aproximadamente 3 mil kilómetros. En cada observatorio se tienen dos túneles de 4 kilómetros de largo cada uno (figura 5). A lo largo de esos túneles viaja, de ida y vuelta, la luz de unos láseres que en los extremos de los túneles se refleja en espejos. Si la distancia entre esos espejos no varía, entonces la comparación entre las propiedades de las luces de cada túnel da siempre el mismo resultado; por ejemplo, que no hay diferencia de colores. No obstante, variaciones muy pequeñas de la distancia entre los espejos, inmediatamente produce un minúsculo cambio en el resultado de tal comparación. ¿Cuán pequeña puede ser la variación de la distancia que se pretende detectar? En el caso que nos ocupa estamos hablando de una 1000000000000000000000 parte de la distancia original, o sea, aproximadamente 0.00000000000001 décimas de milímetro, prácticamente, un millón de veces más pequeño que el átomo más pequeño que conocemos, el átomo de hidrógeno. Ese es el dominio de la física cuántica. Los avances científicos y tecnológicos que ha hecho el equipo de aLigo para lograr medir tales variaciones de distancia (sin confundir la causa con otras que no sean las perturbaciones del espacio-tiempo) son menos imaginables que el Iphone 21.

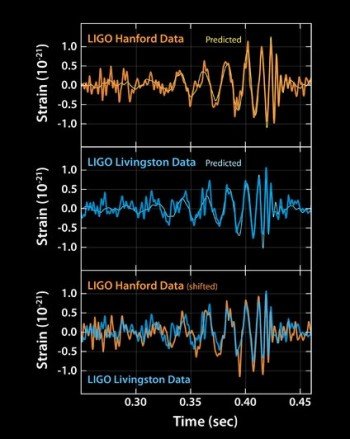
El jueves 11 de febrero, a las 09:30, hora de México, el equipo de aLigo anunció la detección, con una certidumbre científicamente aceptable, de una onda gravitacional; primero en el observatorio de Livingston y luego, como verificación, en el de Hanford. Eso, de por sí, ya sería extraordinario, pero resulta que, al comparar con el catálogo de ondas gravitacionales provisto por la Relatividad Numérica, esta onda no está relacionada con un hoyo negro, ¡sino con dos! En la figura 6, la curva etiquetada con “predicted” muestra el tipo de onda gravitacional que se genera cuando un hoyo negro colisiona con otro hoyo negro y se funden para formar uno solo. Como se puede ver la coincidencia es extraordinaria. En algún lugar muy lejano ubicado hacia el sur de nuestra galaxia, hace unos mil millones de años, dos hoyos negros tuvieron un romance turbulento. La descripción de esa explosiva unión amorosa es, creo, imposible de hacer en otro contexto teórico que no sea el de la Teoría General de la Relatividad.
Esta vez la noticia de la detección de ondas gravitacionales se da después de que el correspondiente artículo científico se aceptó para su publicación en una de las revistas de mayor prestigio en Física en la actualidad (a diferencia de lo que sucedió con BICEP-II, ¿recuerdan?). Esto da mucha credibilidad al hallazgo. Si, finalmente, la comunidad internacional de científicos que trabaja en la teoría y detección de ondas gravitacionales acredita este descubrimiento, no hay dudas de que ameritará el premio Nobel: se corrobora que el espacio-tiempo es un ente dinámico y se corrobora la existencia de los hoyos negros. Entonces, ¿para quién es el premio? C2

